题目内容
当a>0时,设命题P:函数f(x)=x+
在区间(1,2)上单调递增;命题Q:不等式x2+ax+1>0对任意x∈R都成立.若“P且Q”是真命题,则实数a的取值范围是( )
| a |
| x |
| A、0<a≤1 |
| B、1≤a<2 |
| C、0≤a≤2 |
| D、0<a<1或a≥2 |
分析:题中条件:““P且Q”是真命题”,说明P且Q都是真,分别利用导数f′(x)≥0在区间(1,2)上恒成立求出P是真,求出a的取值范围;Q是真时利用二次方程的根的判别式,求出a的取值范围.最后求出交集即得.
解答:解:∵函数f(x)=x+
在区间(1,2)上单调递增;
∴f′(x)≥0在区间(1,2)上恒成立,
∴1-
≥0在区间(1,2)上恒成立,
即a≤x2在区间(1,2)上恒成立,
∴a≤1.且a>0…①
又不等式x2+ax+1>0对任意x∈R都成立,
∴△=a2-4<0,
∴-2<a<2…②
若“P且Q”是真命题,
则P且Q都是真命题,故由①②的交集得:0<a≤1,
则实数a的取值范围是0<a≤1.
故选A.
| a |
| x |
∴f′(x)≥0在区间(1,2)上恒成立,
∴1-
| a |
| x2 |
即a≤x2在区间(1,2)上恒成立,
∴a≤1.且a>0…①
又不等式x2+ax+1>0对任意x∈R都成立,
∴△=a2-4<0,
∴-2<a<2…②
若“P且Q”是真命题,
则P且Q都是真命题,故由①②的交集得:0<a≤1,
则实数a的取值范围是0<a≤1.
故选A.
点评:本小题主要考查函数单调性的应用、逻辑连接词“且”的应用、不等式的恒成立等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.不含逻辑连接词的命题,叫做简单命题.两个简单命题通过“或”、“且”连接或在一个命题前加“非”组成新的命题,叫做复合命题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
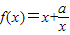 在区间(1,2)上单调递增;命题Q:不等式x2+ax+1>0对任意x∈R都成立.若“P且Q”是真命题,则实数a的取值范围是( )
在区间(1,2)上单调递增;命题Q:不等式x2+ax+1>0对任意x∈R都成立.若“P且Q”是真命题,则实数a的取值范围是( )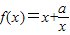 在区间(1,2)上单调递增;命题Q:不等式x2+ax+1>0对任意x∈R都成立.若“P且Q”是真命题,则实数a的取值范围是( )
在区间(1,2)上单调递增;命题Q:不等式x2+ax+1>0对任意x∈R都成立.若“P且Q”是真命题,则实数a的取值范围是( )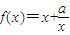 在区间(1,2)上单调递增;命题Q:不等式x2+ax+1>0对任意x∈R都成立.若“P且Q”是真命题,则实数a的取值范围是( )
在区间(1,2)上单调递增;命题Q:不等式x2+ax+1>0对任意x∈R都成立.若“P且Q”是真命题,则实数a的取值范围是( )