题目内容
【题目】如图中的三个直角三角形是一个体积为20cm3的几何体的三视图，则该几何体外接球的面积（单位：cm2）等于（ ）
A.55π
B.75π
C.77π
D.65π
【答案】C
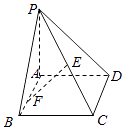
【解析】解：由三视图可知几何体为三棱锥，作出其直观图三棱锥A﹣BCD；
由三视图可知AB⊥平面BCD，BC⊥BD，BD=5，BC=6，AB=h，
∴三棱锥的体积V= 
× 
×5×6h=20，∴h=4；
把三棱锥还原为长方体，如图所示；
则长方体对角线的长是三棱锥外接球的直径2R；
∴（2R）2=42+52+62=77，
∴三棱锥外接球的面积为S=4πR2=77π．
所以答案是：C．
【考点精析】解答此题的关键在于理解由三视图求面积、体积的相关知识，掌握求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积．
练习册系列答案
相关题目
