题目内容
已知曲线y=x3-2x2+5,则在该曲线上,以下哪个点处切线的倾斜角最大
- A.(-2,-11)
- B.(0,5)
- C.(
 ,
,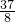 )
) - D.(1,4)
D
分析:先求出函数的导数y′的解析式,再根据函数的导数就是函数在此点的切线的斜率,来求出倾斜角的正切值,从而得出切线的倾斜角最大值.
解答:∵函数的导数y′=3x2-4x,
设切线的倾斜角为α,
∴tanα=3x2-4x,
①当x=-2时,∴tanα=3(-2)2-4(-2)=20,
②当x=0时,∴tanα=3×02-4×0=0,
③当x= 时,∴tanα=3(
时,∴tanα=3( )2-4×(
)2-4×( )=-
)=- ,
,
④当x=1时,∴tanα=3×12-4×1=-1,
又 0≤α<π,
∴当tanα=-1时,切线的倾斜角最大,
此时,x=1,y=4
故选D.
点评:本题考查函数的导数的几何意义,直线的倾斜角和斜率的关系.属于基础题.
分析:先求出函数的导数y′的解析式,再根据函数的导数就是函数在此点的切线的斜率,来求出倾斜角的正切值,从而得出切线的倾斜角最大值.
解答:∵函数的导数y′=3x2-4x,
设切线的倾斜角为α,
∴tanα=3x2-4x,
①当x=-2时,∴tanα=3(-2)2-4(-2)=20,
②当x=0时,∴tanα=3×02-4×0=0,
③当x=
 时,∴tanα=3(
时,∴tanα=3( )2-4×(
)2-4×( )=-
)=- ,
,④当x=1时,∴tanα=3×12-4×1=-1,
又 0≤α<π,
∴当tanα=-1时,切线的倾斜角最大,
此时,x=1,y=4
故选D.
点评:本题考查函数的导数的几何意义,直线的倾斜角和斜率的关系.属于基础题.

练习册系列答案
相关题目
 x3+2与曲线y=4x2-1在x=x处的切线互相垂直,则x的值为 .
x3+2与曲线y=4x2-1在x=x处的切线互相垂直,则x的值为 .