题目内容
已知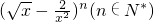 的展开式中第五项的系数与第三项的系数比是10:1.
的展开式中第五项的系数与第三项的系数比是10:1.
(1)求:含 的项的系数; (2)求:展开式中所有项系数的绝对值之和.
的项的系数; (2)求:展开式中所有项系数的绝对值之和.
解: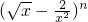 的展开式的通项为
的展开式的通项为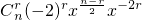 ,
,
∵第五项的系数为Cn4(-2)4,第三项的系数为Cn2(-2)2,
∴Cn4(-2)4=10Cn2(-2)2,化简得(n-2)(n-3)=30,解得:n=8,
∴展开式的通项为Tr+1=
(1)令 ,解得:r=2,∴展开式中含
,解得:r=2,∴展开式中含 的项的系数为:C82(-2)2=112
的项的系数为:C82(-2)2=112
(2)∵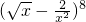 的展开式中所有项系数的绝对值之和,即为
的展开式中所有项系数的绝对值之和,即为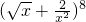 的展开式中所有项的系数和.
的展开式中所有项的系数和.
∴在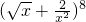 中令x=1得38,故
中令x=1得38,故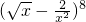 的展开式中所有项系数的绝对值之和为38.
的展开式中所有项系数的绝对值之和为38.
分析:由题意可得Cn4(-2)4=10Cn2(-2)2,可得n=8,从而可得展开式的通项为Tr+1=
(1)令 ,可求r,代入展开式中可求含
,可求r,代入展开式中可求含 的项的系数
的项的系数
(2)可求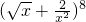 的展开式中所有项的系数和.在
的展开式中所有项的系数和.在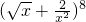 中令x=1可求
中令x=1可求
点评:本题主要考查了利用二项展开式的通项求解展开式的指定的项的系数,及利用赋值法求解二项展开式的各项系数之和,注意本题(2)中的转化.
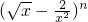 的展开式的通项为
的展开式的通项为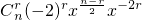 ,
,∵第五项的系数为Cn4(-2)4,第三项的系数为Cn2(-2)2,
∴Cn4(-2)4=10Cn2(-2)2,化简得(n-2)(n-3)=30,解得:n=8,
∴展开式的通项为Tr+1=

(1)令
 ,解得:r=2,∴展开式中含
,解得:r=2,∴展开式中含 的项的系数为:C82(-2)2=112
的项的系数为:C82(-2)2=112(2)∵
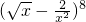 的展开式中所有项系数的绝对值之和,即为
的展开式中所有项系数的绝对值之和,即为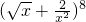 的展开式中所有项的系数和.
的展开式中所有项的系数和.∴在
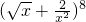 中令x=1得38,故
中令x=1得38,故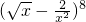 的展开式中所有项系数的绝对值之和为38.
的展开式中所有项系数的绝对值之和为38.分析:由题意可得Cn4(-2)4=10Cn2(-2)2,可得n=8,从而可得展开式的通项为Tr+1=

(1)令
 ,可求r,代入展开式中可求含
,可求r,代入展开式中可求含 的项的系数
的项的系数(2)可求
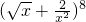 的展开式中所有项的系数和.在
的展开式中所有项的系数和.在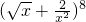 中令x=1可求
中令x=1可求点评:本题主要考查了利用二项展开式的通项求解展开式的指定的项的系数,及利用赋值法求解二项展开式的各项系数之和,注意本题(2)中的转化.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 的展开式中第五项的系数与第三项的系数的比是10:1.
的展开式中第五项的系数与第三项的系数的比是10:1. 的展开式中第五项的系数与第三项的系数的比是10:1
的展开式中第五项的系数与第三项的系数的比是10:1 的项;
的项; 的展开式中第五项的系数与第三项的系数的比是10:1.
的展开式中第五项的系数与第三项的系数的比是10:1. 的展开式中第五项的系数与第三项的系数之比是10︰1,求展开式中x的系数.
的展开式中第五项的系数与第三项的系数之比是10︰1,求展开式中x的系数. 的展开式中第五项的系数与第三项的系数比是10:1.
的展开式中第五项的系数与第三项的系数比是10:1. 的项的系数; (2)求:展开式中所有项系数的绝对值之和.
的项的系数; (2)求:展开式中所有项系数的绝对值之和.