题目内容
侧棱长 为的正三棱锥
为的正三棱锥 的侧面都是直角三角形,且四个顶点都在一个球面上,则球的表面积为( )
的侧面都是直角三角形,且四个顶点都在一个球面上,则球的表面积为( )
A.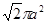 | B.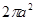 | C.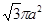 | D.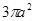 |
D
解析试题分析:因为侧棱长为 的正三棱锥
的正三棱锥 的侧面都是直角三角形,且四个顶点都在一个球面上,三棱锥的定点为正方体的一个角,把三棱锥扩展为正方体,它们有相同的外接球,球的直径就是正方体的对角线,正方体的对角线长为
的侧面都是直角三角形,且四个顶点都在一个球面上,三棱锥的定点为正方体的一个角,把三棱锥扩展为正方体,它们有相同的外接球,球的直径就是正方体的对角线,正方体的对角线长为 ,所以球的表面积为:
,所以球的表面积为: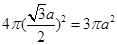 .
.
考点:本题考查三棱锥的外接球的表面积的求法,三棱锥扩展为正方体是本题的关键,正方体的对角线是外接球的直径也不容忽视,考查计算能力.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
右图是边长相等的两个正方形.给定下列三个命题:
①存在三棱柱,其正视图、侧视图如右图;
②存在四棱柱,其正视图、侧视图如右图;
③存在圆柱,其正视图、侧视图如右图.
其中真命题的个数是
| A.3 | B.2 | C.1 | D.0 |
已知一个几何体的三视图如图所示,则这个几何体的体积是( )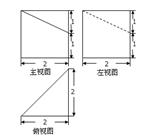
A.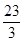 | B.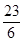 | C. | D.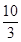 |
若正方体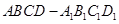 的外接球
的外接球 的体积为
的体积为 ,则球心
,则球心 到正方体的一个面
到正方体的一个面 的距离为( )
的距离为( )
| A.1 | B.2 | C.3 | D.4 |
一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为( ) .
.
A. | B. | C. | D. |
已知正四棱锥的各棱棱长都为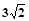 ,则正四棱锥的外接球的表面积为( )
,则正四棱锥的外接球的表面积为( )
A.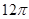 | B.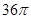 | C. | D.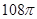 |
如图所示,则根据图中数据可知该几何体的体积为( ).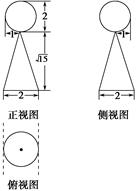
| A.8π | B.9π | C.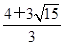 π π | D.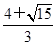 π π |
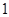 的正方形
的正方形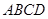 沿对角线
沿对角线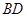 折起,使得平面
折起,使得平面 平面
平面 ,形成三棱锥
,形成三棱锥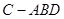 的正视图与俯视图如下图所示,则侧视图的面积为 ( )
的正视图与俯视图如下图所示,则侧视图的面积为 ( )


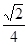
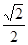
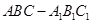 的六个顶点都在半径为1的半球面上,
的六个顶点都在半径为1的半球面上, ,侧面
,侧面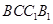 是半球底面圆的内接正方形,则侧面
是半球底面圆的内接正方形,则侧面 的面积为( )
的面积为( )