题目内容
如图，一艘船上午9：30在A处测得灯塔S在它的北偏东30°处，之后它继续沿正北方向匀速航行，上午10：00到达B处，此时又测得灯塔S在它的北偏东75°处，且与它相距8
n mile．此船的航速是 n mile/h．
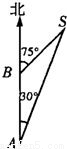
【答案】分析：由题意及图形在△ABS中，已知∠BAS=30°，∠ASB=45°，又已知三角形ABS中边BS=8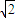
，先求出边AB的长，再利用物理知识解出．
解答：解：因为在△ABS中，已知∠BAS=30°，∠ASB=45°，且边BS=8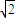
，利用正弦定理可得：
?
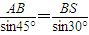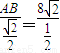⇒AB=16，
又因为从A到S匀速航行时间为半个小时，所以速度应为：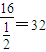
（mile/h）．
故答案为：32．
点评：此题考查了学生的物理知识速度=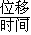
，还考查了正弦定理求解三角形及三角形外角等与不相邻的两内角和．
，先求出边AB的长，再利用物理知识解出．解答：解：因为在△ABS中，已知∠BAS=30°，∠ASB=45°，且边BS=8
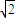，利用正弦定理可得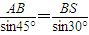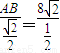：?⇒AB=16，又因为从A到S匀速航行时间为半个小时，所以速度应为：
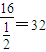（mile/h）．故答案为：32．
点评：此题考查了学生的物理知识速度=
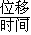，还考查了正弦定理求解三角形及三角形外角等与不相邻的两内角和． 
练习册系列答案
相关题目
如图，一艘船上午9：30在A处测得灯塔S在它的北偏东30°处，之后它继续沿正北方向匀速航行，上午10：00到达B处，此时又测得灯塔S在它的北偏东75°处，且与它相距8