题目内容
(本题满分12分)若定义在 上的函数
上的函数 同时满足下列三个条件:
同时满足下列三个条件:
①对任意实数 均有
均有 成立;
成立;
② ; ③当
; ③当 时,都有
时,都有 成立。
成立。
(1)求 ,
, 的值;
的值;
(2)求证: 为
为 上的增函数
上的增函数
(3)求解关于 的不等式
的不等式 .
.
【答案】
(1)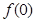 =0,
=0, 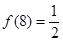 ;(2)证明:见解析;(3)
;(2)证明:见解析;(3)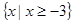 .
.
【解析】本试题主要是考查了函数的单调性的证明,以及函数与不等式的求解,赋值法求解函数的值。
(1)令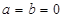 得
得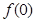 =0,令
=0,令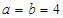 ,得
,得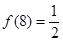
(2)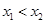 则
则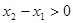 ,则
,则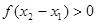 ;利用已知关系式
;利用已知关系式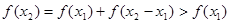 得到证明
得到证明
(3)在第二问的基础上可知得到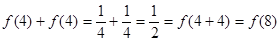 ,转换不等式得到
,转换不等式得到
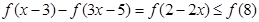 ,进而求解得到结论。
,进而求解得到结论。
解:(1)令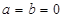 得
得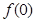 =0,令
=0,令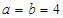 ,得
,得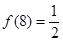
(2)证明:设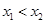 则
则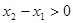 ,则
,则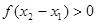 ;
;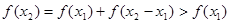 ,故
,故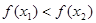 ,
,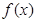 为R上的增函数
为R上的增函数
(3)由已知得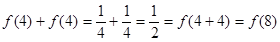 原不等式转化为
原不等式转化为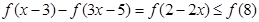 ,结合
,结合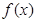 为R上的增函数得:
为R上的增函数得:
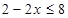 ,解得
,解得 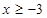 .故原不等式的解集为
.故原不等式的解集为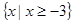 .
.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
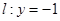 相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点
相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点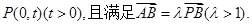
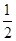 ,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;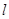 上,求证:t与
上,求证:t与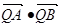 均为定值。
均为定值。 ,且
,且 ,
求实数
,
求实数 的值.
的值.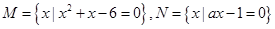 ,且
,且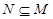 ,
求实数
,
求实数 的值.
的值. 有最大值9和最小值3,求实数
有最大值9和最小值3,求实数 的值
的值