题目内容
附加题（本题猜测正确1分，证明正确5分）
若
，观察下列不等式：
请你猜测
满足的不等式，并用数学归纳法加以证明.
略
解析:
满足的不等式为
,证明如下：
(
1)当n=2时，猜想成立；
(2)假设当n=k时，猜想成立，即
，
那么n=k+1时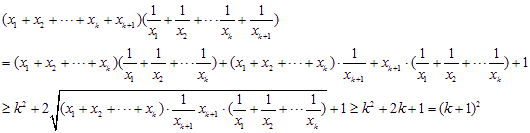
则当n=k+1时猜想也成立，根据(1)(2)可得猜想对任意的n(n
)都成立.
练习册系列答案
相关题目
解析:
题目内容
附加题（本题猜测正确1分，证明正确5分）
若，观察下列不等式：
请你猜测满足的不等式，并用数学归纳法加以证明.
略
满足的不等式为 ,证明如下：
(1)当n=2时，猜想成立；
(2)假设当n=k时，猜想成立，即，
那么n=k+1时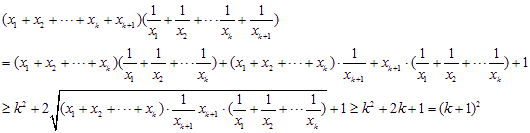
则当n=k+1时猜想也成立，根据(1)(2)可得猜想对任意的n(n)都成立.
，观察下列不等式：
满足的不等式，并用数学归纳法加以证明.