题目内容
设数列an的前n项的和为Sn,a1=1,2Sn=(n+1)an+1-1
(1)求数列an的通项公式;
(3)求证:数列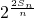 是等比数列;
是等比数列;
(3)设数列bn是等比数列且b1=2,a1,a3,b2成等比数列,Tm为bn的前m项的和,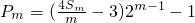 ,试比较Tm与Pm的大小,并加以证明.
,试比较Tm与Pm的大小,并加以证明.
解:(1)当n≥2时,2an=2Sn-2Sn-1=(n+1)an+1-1-(nan-1)
即(n+1)an+1=(n+2)an即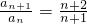 (2分)
(2分)
而当n=1时,2S1=2a2-1,
∴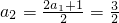 ,(3分)
,(3分)
∴
而当n=1时,a1=1符合上式,综上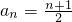 (4分)
(4分)
(2)证明:由(1)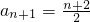 ,
,
∴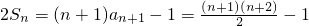
∴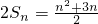 (6分)
(6分)
∴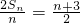
∴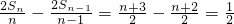
∴当n≥2时
∴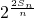 是以2为首项
是以2为首项 为公比的等比数列..(8分)
为公比的等比数列..(8分)
(3)由(1)a3=2
∵a1,a3,b2成等比数列∴a1b2=a32
∴b2=4
∴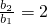
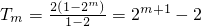 (9分)
(9分)
而由(2)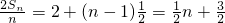
∴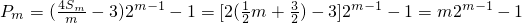 .(10分)
.(10分)
∴Pm-Tm=m•2m-1-1-(2m+1-2)=(m-4)•2m-1+1
当1≤m≤3且n∈N*时,Pm<Tm
当m≥4且n∈N*时,Pm>Tm(12分)
分析:(1)当n≥2时,2an=2Sn-2Sn-1=(n+1)an+1-1-(nan-1),即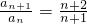 ,而当n=1时,2S1=2a2-1,
,而当n=1时,2S1=2a2-1, ,当n=1时,a1=1符合上式,故
,当n=1时,a1=1符合上式,故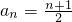 .
.
(2)由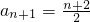 ,知
,知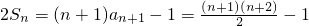 ,
,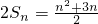 ,
,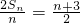 ,
,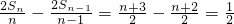 ,由此能够证明
,由此能够证明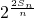 是以2为首项
是以2为首项 为公比的等比数列.
为公比的等比数列.
(3)由a3=2,a1,a3,b2成等比数列,知b2=4,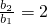
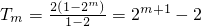 ,由此入手能够得到当1≤m≤3且n∈N*时,Pm<Tm,当m≥4且n∈N*时,Pm>Tm.
,由此入手能够得到当1≤m≤3且n∈N*时,Pm<Tm,当m≥4且n∈N*时,Pm>Tm.
点评:本题考查数列的通项公式的求法、等比数列的证明和数列前m项和的比较,解题时要认真审题,注意挖掘隐含条件.
即(n+1)an+1=(n+2)an即
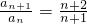 (2分)
(2分)而当n=1时,2S1=2a2-1,
∴
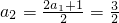 ,(3分)
,(3分)∴

而当n=1时,a1=1符合上式,综上
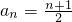 (4分)
(4分)(2)证明:由(1)
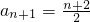 ,
,∴
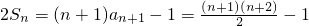
∴
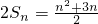 (6分)
(6分)∴
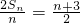
∴
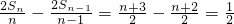
∴当n≥2时

∴
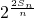 是以2为首项
是以2为首项 为公比的等比数列..(8分)
为公比的等比数列..(8分)(3)由(1)a3=2
∵a1,a3,b2成等比数列∴a1b2=a32
∴b2=4
∴
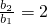
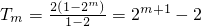 (9分)
(9分)而由(2)
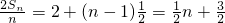
∴
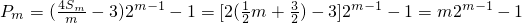 .(10分)
.(10分)∴Pm-Tm=m•2m-1-1-(2m+1-2)=(m-4)•2m-1+1
当1≤m≤3且n∈N*时,Pm<Tm
当m≥4且n∈N*时,Pm>Tm(12分)
分析:(1)当n≥2时,2an=2Sn-2Sn-1=(n+1)an+1-1-(nan-1),即
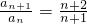 ,而当n=1时,2S1=2a2-1,
,而当n=1时,2S1=2a2-1, ,当n=1时,a1=1符合上式,故
,当n=1时,a1=1符合上式,故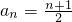 .
.(2)由
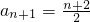 ,知
,知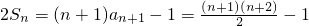 ,
,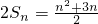 ,
,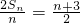 ,
,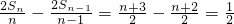 ,由此能够证明
,由此能够证明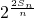 是以2为首项
是以2为首项 为公比的等比数列.
为公比的等比数列.(3)由a3=2,a1,a3,b2成等比数列,知b2=4,
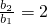
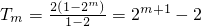 ,由此入手能够得到当1≤m≤3且n∈N*时,Pm<Tm,当m≥4且n∈N*时,Pm>Tm.
,由此入手能够得到当1≤m≤3且n∈N*时,Pm<Tm,当m≥4且n∈N*时,Pm>Tm.点评:本题考查数列的通项公式的求法、等比数列的证明和数列前m项和的比较,解题时要认真审题,注意挖掘隐含条件.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 .
. ,求数列{an}的通项公式;
,求数列{an}的通项公式; .
. ,求数列{an}的通项公式;
,求数列{an}的通项公式; .
. ,求数列{an}的通项公式;
,求数列{an}的通项公式; .
. ,求数列{an}的通项公式;
,求数列{an}的通项公式;