题目内容
11.解不等式:(1)lg(x-1)<1;
(2)a2x-7>a4x-1(a>0,且a≠1)
分析 (1)原不等式等价于lg(x-1)<lg10,由对数函数的单调性可得;
(2)分类讨论:当a>1和0<a<1时,分别由对数函数的单调性可得.
解答 解:(1)原不等式等价于lg(x-1)<lg10,
由对数函数的单调性可得0<x-1<10,
解得1<x<11,
∴原不等式的解集为{x|1<x<11};
(2)当a>1时,由a2x-7>a4x-1可得2x-7>4x-1,解得x<-3,
∴不等式的解集为{x|x<-3};
当0<a<1时,由a2x-7>a4x-1可得2x-7<4x-1,解得x>-3,
∴不等式的解集为{x|x>-3}.
点评 本题考查指数对数不等式的解集,涉及分类讨论的思想和函数的单调性,属基础题.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
1.函数y=1+sinx的部分图象如图所示,则该函数在[0,2π]的单调递减区间是( )
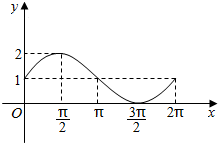

| A. | [0,π] | B. | [$\frac{π}{2}$,$\frac{3π}{2}$] | C. | [0,$\frac{3π}{2}$] | D. | [$\frac{π}{2}$,2π] |
2.点A、B、C、D在同一个球的球面上,${A}{B}={B}C=\sqrt{2}$,AC=2,若四面体ABCD体积的最大值为$\frac{2}{3}$,则这个球的表面积为( )
| A. | 8π | B. | $\frac{25π}{4}$ | C. | $\frac{25π}{16}$ | D. | $\frac{125π}{6}$ |
6.f(x)是定义在R上的奇函数,且f(3)>f(1),下列各式一定成立的是( )
| A. | f(0)<f(4) | B. | f(-3)<f(-1) | C. | f(-1)<f(-3) | D. | f(3)>f(0) |