题目内容
完成下列各小题.
(1)函数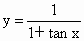 的定义域是___________;
的定义域是___________;
(2)函数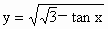 的定义域为_______,值域为_______;
的定义域为_______,值域为_______;
(3)函数y=tan(sinx)的定义域为___________,值域为__________.
解析:
|
解: (1)要使函数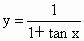 有意义, 有意义,
则 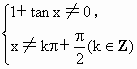 即 即 ,且 ,且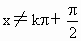 (kÎ
Z) (kÎ
Z)
∴函数的定义域为 {x|xÎ R 且 , ,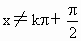 ,kÎ
Z}. ,kÎ
Z}.
(2) ∵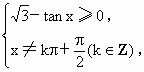
∴ 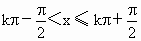 (kÎ
Z). (kÎ
Z).
显然值域为 [0,+∞).(3) ∵-1≤sinx≤1,∴xÎ R,yÎ [-tan1,tan1],答案: (1){xÎ R且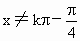 , ,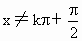 ,kÎ
Z}; ,kÎ
Z};
(2)( 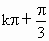 )(kÎ
Z),[0,+∞); )(kÎ
Z),[0,+∞);
(3)R ,[-tan1,tan1]根据求定义域的基本原则及三角函数本身的限制求解. 解答本题要注意掌握好基本函数 y=tanx的定义域、值域、单调性等知识. |

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案(本小题满分12分)
某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(Ⅰ)A类工人中和B类工人各抽查多少工人?
(Ⅱ)从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
| 生产能力分组 |
|
|
|
|
|
| 人数 | 4 | 8 |
| 5 | 3 |
表2:
| 生产能力分组 |
|
|
|
|
| 人数 | 6 | y | 36 | 18 |
(ⅰ)先确定![]() ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
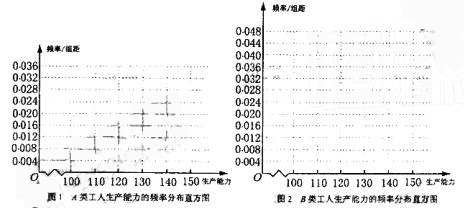
(ii)分别估计![]() 类工人和
类工人和![]() 类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)。
类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)。
(本小题满分13分)某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
|
组号 |
分组 |
频数 |
频率 |
|
第1组 |
|
5 |
0.050 |
|
第2组 |
|
① |
0.350 |
|
第3组 |
|
30 |
② |
|
第4组 |
|
20 |
0.200 |
|
第5组 |
|
10 |
0.100 |
|
合计 |
100 |
1.00 |

((本小题满分12分)某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
|
组号 |
分组 |
频数 |
频率 |
|
第1组 |
|
5 |
0.050 |
|
第2组 |
|
① |
0.350 |
|
第3组 |
|
30] |
② |
|
第4组 |
|
20 |
0.200 |
|
第5组 |
|
10 |
0.100 |
|
合计 |
100 |
1.00 |
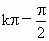
 的定义域是___________;
的定义域是___________;
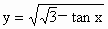 的定义域为_______,值域为_______;
的定义域为_______,值域为_______;