题目内容
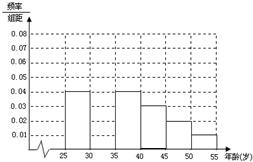某班同学利用五一节进行社会实践，对[25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念，则称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：| 组数 | 分组 | 低碳族 的人数 |
占本组 的频率 |
| 1 | [25，30） | 120 | 0.6 |
| 2 | [30，35） | 195 | P |
| 3 | [35，40） | 100 | 0.5 |
| 4 | [40，45） | a | 0.4 |
| 5 | [45，50） | 30 | 0.3 |
| 6 | [50，55） | 15 | 0.3 |
（2）在所得样本中，从[40，50）岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁的人数为X，求X的分布列和数学期望EX．
分析：（I）由题意及统计图表，利用图表性质得第二组的频率为1-（0.04+0.04+0.03+0.02+0.01）×5=0.3，在有频率定义知高为
=0.06，在有频率分布直方图会全图形即可；
（II）由题意及（I）因为[40，45）岁年龄段的“低碳族”与[45，50）岁年龄段的“低碳族”的比值为60：30=2：1，所以采用分层抽样法抽取18人，[40，45）岁中有12人，[45，50）岁中有6人，并且由题意分出随机变量X服从超几何分布，利用分布列定义可以求出分布列，并利用分布列求出期望．
| 0.3 |
| 5 |
（II）由题意及（I）因为[40，45）岁年龄段的“低碳族”与[45，50）岁年龄段的“低碳族”的比值为60：30=2：1，所以采用分层抽样法抽取18人，[40，45）岁中有12人，[45，50）岁中有6人，并且由题意分出随机变量X服从超几何分布，利用分布列定义可以求出分布列，并利用分布列求出期望．
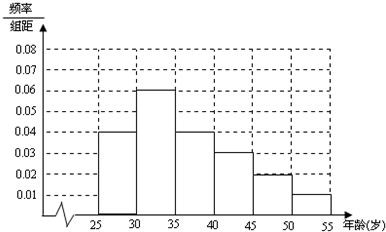
解答：解：（Ⅰ）第二组的频率为1-（0.04+0.04+0.03+0.02+0.01）×5=0.3，所以高为
=0.06．
频率直方图如下：
第一组的人数为
=200，频率为0.04×5=0.2，所以n=
=1000．
由题可知，第二组的频率为0.3，所以第二组的人数为1000×0.3=300，所以p=
=0.65．
第四组的频率为0.03×5=0.15，所以第四组的人数为1000×0.15=150，所以a=150×0.4=60．
（Ⅱ）因为[40，45）岁年龄段的“低碳族”与[45，50）岁年龄段的“低碳族”的比值为60：30=2：1，所以采用分层抽样法抽取18人，[40，45）岁中有12人，[45，50）岁中有6人．
随机变量X服从超几何分布．P(X=0)=
=
，P(X=1)=
=
，P(X=2)=
=
，P(X=3)=
=
．
所以随机变量X的分布列为
∴数学期望EX=0×
+1×
+2×
+3×
=2．
| 0.3 |
| 5 |
频率直方图如下：
第一组的人数为
| 120 |
| 0.6 |
| 200 |
| 0.2 |
由题可知，第二组的频率为0.3，所以第二组的人数为1000×0.3=300，所以p=
| 195 |
| 300 |
第四组的频率为0.03×5=0.15，所以第四组的人数为1000×0.15=150，所以a=150×0.4=60．
（Ⅱ）因为[40，45）岁年龄段的“低碳族”与[45，50）岁年龄段的“低碳族”的比值为60：30=2：1，所以采用分层抽样法抽取18人，[40，45）岁中有12人，[45，50）岁中有6人．
随机变量X服从超几何分布．P(X=0)=
| ||||
|
| 5 |
| 204 |
| ||||
|
| 15 |
| 68 |
| ||||
|
| 33 |
| 68 |
| ||||
|
| 55 |
| 204 |
所以随机变量X的分布列为
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 5 |
| 204 |
| 15 |
| 68 |
| 33 |
| 68 |
| 55 |
| 204 |
点评：此题考查了频率分布直方图及其性质，还考查了统计中的分层抽样及离散型随机变量的定义及分布列，并考查了应用其分布列求其期望，重在考查学生的理解及计算能力．
练习册系列答案
相关题目
某班同学利用五一节进行社会实践，对[25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念，则称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：
| 组数 | 分组 | 低碳族 的人数 | 占本组 的频率 |
| 1 | [25，30） | 120 | 0.6 |
| 2 | [30，35） | 195 | P |
| 3 | [35，40） | 100 | 0.5 |
| 4 | [40，45） | a | 0.4 |
| 5 | [45，50） | 30 | 0.3 |
| 6 | [50，55） | 15 | 0.3 |
（2）在所得样本中，从[40，50）岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁的人数为X，求X的分布列和数学期望EX．
某班同学利用五一节进行社会实践，对[25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念，则称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：
（1）请补全频率分布直方图，并求n、a、p的值；
（2）在所得样本中，从[40，50）岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁的人数为X，求X的分布列和数学期望EX．
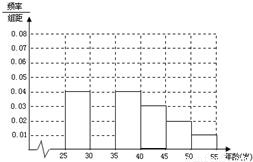
| 组数 | 分组 | 低碳族 的人数 | 占本组 的频率 |
| 1 | [25，30） | 120 | 0.6 |
| 2 | [30，35） | 195 | P |
| 3 | [35，40） | 100 | 0.5 |
| 4 | [40，45） | a | 0.4 |
| 5 | [45，50） | 30 | 0.3 |
| 6 | [50，55） | 15 | 0.3 |
（2）在所得样本中，从[40，50）岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁的人数为X，求X的分布列和数学期望EX．
某班同学利用五一节进行社会实践，对[25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念，则称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：
（1）请补全频率分布直方图，并求n、a、p的值；
（2）在所得样本中，从[40，50）岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁的人数为X，求X的分布列和数学期望EX．
| 组数 | 分组 | 低碳族 的人数 | 占本组 的频率 |
| 1 | [25，30） | 120 | 0.6 |
| 2 | [30，35） | 195 | P |
| 3 | [35，40） | 100 | 0.5 |
| 4 | [40，45） | a | 0.4 |
| 5 | [45，50） | 30 | 0.3 |
| 6 | [50，55） | 15 | 0.3 |
（2）在所得样本中，从[40，50）岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁的人数为X，求X的分布列和数学期望EX．
某班同学利用五一节进行社会实践，对[25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念，则称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：
（1）请补全频率分布直方图，并求n、a、p的值；
（2）在所得样本中，从[40，50）岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁的人数为X，求X的分布列和数学期望EX．
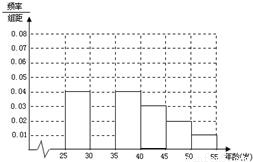
| 组数 | 分组 | 低碳族 的人数 | 占本组 的频率 |
| 1 | [25，30） | 120 | 0.6 |
| 2 | [30，35） | 195 | P |
| 3 | [35，40） | 100 | 0.5 |
| 4 | [40，45） | a | 0.4 |
| 5 | [45，50） | 30 | 0.3 |
| 6 | [50，55） | 15 | 0.3 |
（2）在所得样本中，从[40，50）岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁的人数为X，求X的分布列和数学期望EX．