题目内容
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号恰好相同的概率;
(Ⅱ)求取出的两个球上的标号至少有一个大于2的概率.
解:利用树状图可以列出从甲、乙两个盒子中各取出1个球的所有可能结果:
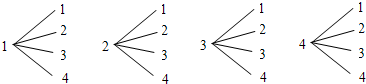
可以看出,试验的所有可能结果数为16种且每种结果是等可能的.
(Ⅰ)所取两个小球上的标号为相同整数的结果
有1-1,2-2,3-3,4-4,共4种.
故根据古典概型公式,所求概率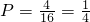 .
.
答:取出的两个小球上的标号为相邻整数的概率为 .
.
(Ⅱ)记事件“取出的两个球上的标号至少有一个大于2”为A
则A的对立事件是 =“取出的两个球上的标号都不于大2”
=“取出的两个球上的标号都不于大2”
所取出的两个球上的标号都不大于3的结果有1-1,1-2,2-1,2-2,
共4种.(10分)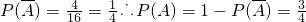 .
.
答:取出的两个球上的标号至少有一个大于3的概率为 .
.
(注:利用列表或列数对的方法求解以及II直接列出A的结果,仿照上述解法给分)
分析:利用树状图可以列出从甲、乙两个盒子中各取出1个球的所有可能结果
(I)所取两个小球上的标号为相同整数的结果
有1-1,2-2,3-3,4-4,共4种.根据古典概型公式,求概率
(Ⅱ)由于取出的两个球上的标号至少有一个大于2的情况较多故考虑对立事件:取出的两个球上的标号都不于大2
即取出的两个球上的标号都不大于3的结果有1-1,1-2,2-1,2-2,利用对立事件的概率公式.
点评:本题主要考查了利用树状图找出试验的所有结果数,考查了古典概率的计算公式的应用,对立事件的概率公式的运用.
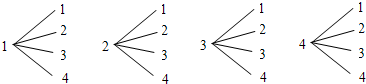
可以看出,试验的所有可能结果数为16种且每种结果是等可能的.
(Ⅰ)所取两个小球上的标号为相同整数的结果
有1-1,2-2,3-3,4-4,共4种.
故根据古典概型公式,所求概率
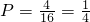 .
.答:取出的两个小球上的标号为相邻整数的概率为
 .
.(Ⅱ)记事件“取出的两个球上的标号至少有一个大于2”为A
则A的对立事件是
 =“取出的两个球上的标号都不于大2”
=“取出的两个球上的标号都不于大2”所取出的两个球上的标号都不大于3的结果有1-1,1-2,2-1,2-2,
共4种.(10分)
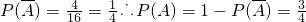 .
.答:取出的两个球上的标号至少有一个大于3的概率为
 .
.(注:利用列表或列数对的方法求解以及II直接列出A的结果,仿照上述解法给分)
分析:利用树状图可以列出从甲、乙两个盒子中各取出1个球的所有可能结果
(I)所取两个小球上的标号为相同整数的结果
有1-1,2-2,3-3,4-4,共4种.根据古典概型公式,求概率
(Ⅱ)由于取出的两个球上的标号至少有一个大于2的情况较多故考虑对立事件:取出的两个球上的标号都不于大2
即取出的两个球上的标号都不大于3的结果有1-1,1-2,2-1,2-2,利用对立事件的概率公式.
点评:本题主要考查了利用树状图找出试验的所有结果数,考查了古典概率的计算公式的应用,对立事件的概率公式的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的三个大小相同的球,现从甲、乙两个盒子中各取出
的三个大小相同的球,现从甲、乙两个盒子中各取出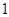 个球,每个球被取出的可能性相等.
个球,每个球被取出的可能性相等. 的概率.
的概率.