题目内容
(本题满分12分)
在△ABC中,角A、B、C所对的边分别为a、b、c(其中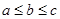 ),设向量
),设向量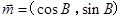 ,
,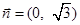 ,且向量
,且向量 为单位向量.(模为1的向量称作单位向量)
为单位向量.(模为1的向量称作单位向量)
(1)求∠B的大小;
(2)若 ,求△ABC的面积.
,求△ABC的面积.
在△ABC中,角A、B、C所对的边分别为a、b、c(其中
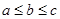 ),设向量
),设向量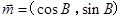 ,
,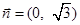 ,且向量
,且向量 为单位向量.(模为1的向量称作单位向量)
为单位向量.(模为1的向量称作单位向量)(1)求∠B的大小;
(2)若
 ,求△ABC的面积.
,求△ABC的面积.(1)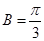 ;(2)C=
;(2)C=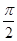 ,△ABC的面积=
,△ABC的面积=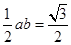 。
。
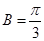 ;(2)C=
;(2)C=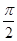 ,△ABC的面积=
,△ABC的面积=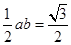 。
。本试题主要是考查了向量的数量积和解三角形中边角转换的运用。
(1)根据两个向量的坐标,以及差向量的模长为1,结合数量积的性质可知得到角B的值。
(2)正弦定理可知sinA,然后又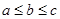 ,∴
,∴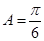 ,结合正弦面积公式得到结论。
,结合正弦面积公式得到结论。
解:(1)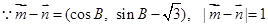 --------------------2分
--------------------2分
∴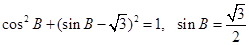 --------------------4分
--------------------4分
又B为三角形的内角,由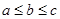 ,故
,故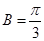 --------------------6分
--------------------6分
(2)根据正弦定理,知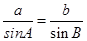 ,即
,即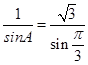 ,
,
∴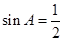 ,又
,又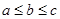 ,∴
,∴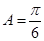 --------------------9分
--------------------9分
故C=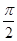 ,△ABC的面积=
,△ABC的面积=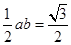 ----------------------12分
----------------------12分
(1)根据两个向量的坐标,以及差向量的模长为1,结合数量积的性质可知得到角B的值。
(2)正弦定理可知sinA,然后又
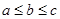 ,∴
,∴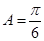 ,结合正弦面积公式得到结论。
,结合正弦面积公式得到结论。解:(1)
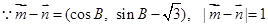 --------------------2分
--------------------2分∴
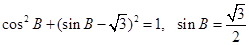 --------------------4分
--------------------4分又B为三角形的内角,由
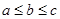 ,故
,故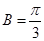 --------------------6分
--------------------6分(2)根据正弦定理,知
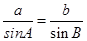 ,即
,即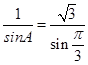 ,
,∴
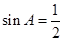 ,又
,又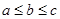 ,∴
,∴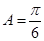 --------------------9分
--------------------9分故C=
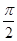 ,△ABC的面积=
,△ABC的面积=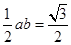 ----------------------12分
----------------------12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
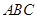 中
中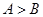 ,给出下列不等式:
,给出下列不等式: 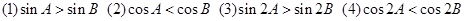
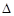 ABC中,已知
ABC中,已知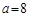 ,
,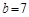 ,
,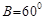 ,求
,求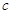 .
.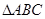 中,角A,B,C所对的边分别是
中,角A,B,C所对的边分别是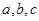 ,且
,且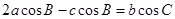 。
。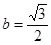 ,求周长
,求周长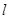 的最大值。
的最大值。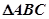 的面积为
的面积为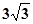 ,
,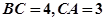 ,则边
,则边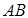 的大小为
的大小为 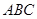 中,角
中,角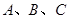 的对边分别为
的对边分别为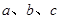 ,且
,且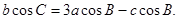
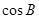 的值;
的值;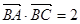 ,且
,且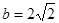 ,求
,求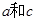 的值.
的值.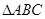 中,
中,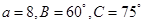 ,则
,则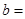 ( )
( )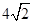
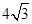
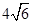
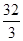
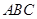 中,若
中,若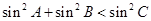 ,则△
,则△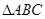 的三个内角
的三个内角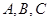 所对的边分别是
所对的边分别是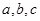 ,且
,且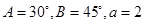 ,则
,则 .
.