题目内容
【题目】设函数f(x)=log2(4x)log2(2x)的定义域为 ![]() . (Ⅰ)若t=log2x,求t的取值范围;
. (Ⅰ)若t=log2x,求t的取值范围;
(Ⅱ)求y=f(x)的最大值与最小值,并求取得最值时对应的x的值.
【答案】解:(Ⅰ)∵t=log2x, ![]() ≤x≤4, ∴log2
≤x≤4, ∴log2![]() ≤t≤log24,
≤t≤log24,
∴﹣2≤t≤2,即t的取值范围是[﹣2,2]
(Ⅱ)f(x)=log2(4x)log2(2x)=(log24+log2x)(log22+log2x)
=(2+log2x)(1+log2x)=(2+t)(1+t)
=t2+3t+2=(t+ ![]() )2﹣
)2﹣ ![]() ,
,
∵﹣2≤t≤2,
当x=4时,最大值为12; ![]() 时,最小值-
时,最小值- ![]()
【解析】(Ⅰ)利用对数函数的单调性,若t=log2x,求t的取值范围;(Ⅱ)利用对数的运算法则,结合配方法,即可得出结论.
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.

练习册系列答案
相关题目
【题目】某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量 | 100 | 94 | 93 | 90 | 85 | 78 |
(1)求回归直线方程![]() ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润![]() 销售收入
销售收入![]() 成本)(附:对于一组数据
成本)(附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: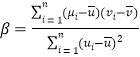 ,
,![]() ),
),![]() ,
,![]()