题目内容
已知
(xcosx+3a-b)dx=2a+6,f(t)=
(x3+ax+5a-b)dx为偶函数,则a+b=( )
| ∫ | 1 -1 |
| ∫ | t 0 |
| A、-6 | B、-12 | C、4 | D、-4 |
分析:先计算∫-11(xcosx+3a-b)dx得出6a-2b=2a+6,?2a-b=3,①再由f(t)=∫0t(x3+ax+5a-b)dx结合偶函数,得出5a-b=0,②最后由①②得:a=-1,b=-5.从而求得a+b的值.
解答:解:∵∫-11(xcosx+3a-b)dx=2a+6,
即(xsinx+cosx+3ax-bx)|-11=2a+6,
6a-2b=2a+6,?2a-b=3,①
又f(t)=∫0t(x3+ax+5a-b)dx
即:f(t)=(
x4+
ax 2+5ax-bx)|
=
t4+
at 2+5at-bt
因为偶函数,∴5a-b=0,②
由①②得:a=-1,b=-5.
则a+b=-6.
故选A.
即(xsinx+cosx+3ax-bx)|-11=2a+6,
6a-2b=2a+6,?2a-b=3,①
又f(t)=∫0t(x3+ax+5a-b)dx
即:f(t)=(
| 1 |
| 4 |
| 1 |
| 2 |
t 0 |
| 1 |
| 4 |
| 1 |
| 2 |
因为偶函数,∴5a-b=0,②
由①②得:a=-1,b=-5.
则a+b=-6.
故选A.
点评:本小题主要考查定积分、函数奇偶性的应用、方程组的解法等基础知识,考查运算求解能力,化归与转化思想.属于基础题.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
等差数列{an}的前n项和为Sn,公差为d,已知(a8+1)3+2013(a8+1)=1,(a2006+1)3+2013(a2006+1)=-1,则下列结论正确的是( )
| A、d<0,S2013=2013 | B、d>0,S2013=2013 | C、d<0,S2013=-2013 | D、d>0,S2013=-2013 |
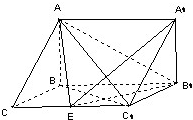 如图,在三棱柱△ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,BB1=2,∠BCC1=
如图,在三棱柱△ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,BB1=2,∠BCC1=