题目内容
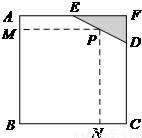
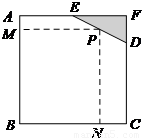
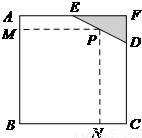
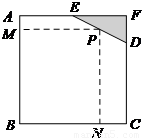
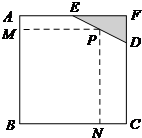 如图所示,已知边长为8米的正方形钢板有一个角被锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.
如图所示,已知边长为8米的正方形钢板有一个角被锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.(Ⅰ)设MP=x米,PN=y米,将y表示成x的函数,求该函数的解析式及定义域;
(Ⅱ)求矩形BNPM面积的最大值.
分析:(I)利用三角形的相似,可得函数的解析式及定义域;
(Ⅱ)表示出面积,利用配方法,可得矩形BNPM面积的最大值.
(Ⅱ)表示出面积,利用配方法,可得矩形BNPM面积的最大值.
解答:解:(I)作PQ⊥AF于Q,所以PQ=8-y,EQ=x-4…(2分)
在△EDF中,
=
,所以
=
…(4分)
所以y=-
x+10,定义域为{x|4≤x≤8}…(6分)
(II)设矩形BNPM的面积为S,则S(x)=xy=x(10-
)=-
(x-10)2+50…(9分)
所以S(x)是关于x的二次函数,且其开口向下,对称轴为x=10
所以当x∈[4,8],S(x)单调递增 …(11分)
所以当x=8米时,矩形BNPM面积取得最大值48平方米 …(13分)
在△EDF中,
| EQ |
| PQ |
| EF |
| FD |
| x-4 |
| 8-y |
| 4 |
| 2 |
所以y=-
| 1 |
| 2 |
(II)设矩形BNPM的面积为S,则S(x)=xy=x(10-
| x |
| 2 |
| 1 |
| 2 |
所以S(x)是关于x的二次函数,且其开口向下,对称轴为x=10
所以当x∈[4,8],S(x)单调递增 …(11分)
所以当x=8米时,矩形BNPM面积取得最大值48平方米 …(13分)
点评:本题考查函数解析式的确定,考查配方法求函数的最值,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目