题目内容
将函数f(x)=tan(2x+
)+1按向量
平移得到奇函数g(x),要使|
|最小,则
=( )
| π |
| 3 |
| a |
| a |
| a |
A、(
| ||
B、(-
| ||
C、(
| ||
D、(-
|
分析:函数的图象平移后是奇函数,必须是正切函数,先向下平移,再向右平移-
+
(k∈Z)个单位,选择适当的k即可求出
.
| kπ |
| 2 |
| π |
| 6 |
| a |
解答:解:要经过平移得到奇函数g(x),应将函数f(x)=tan(2x+
)+1的图象向下平移1个单位,
再向右平移-
+
(k∈Z)个单位.即应按照向量
=(-
+
,-1) (k∈Z)进行平移.
要使|
|最小,只需k=0即可,所以
=(
,-1)
故选A.
| π |
| 3 |
再向右平移-
| kπ |
| 2 |
| π |
| 6 |
| a |
| kπ |
| 2 |
| π |
| 6 |
要使|
| a |
| a |
| π |
| 6 |
故选A.
点评:本题是基础题,考查正切函数的奇偶性与对称性,考查函数图象的平移,注意向量的平移的方向.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )+1按向量
)+1按向量 平移得到奇函数g(x),要使|
平移得到奇函数g(x),要使| ,-1)
,-1) ,1)
,1)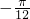 ,-1)
,-1)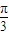 )+1按向量
)+1按向量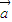 平移得到奇函数g(x),要使|
平移得到奇函数g(x),要使|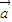 |最小,则
|最小,则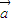 =( )
=( )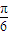 ,-1)
,-1)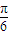 ,1)
,1)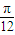 ,1)
,1) ,-1)
,-1)