题目内容
设抛物线C: 的焦点为F,经过点F的直线与抛物线交于A、B两点.
的焦点为F,经过点F的直线与抛物线交于A、B两点.
(1)若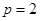 ,求线段
,求线段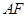 中点M的轨迹方程;
中点M的轨迹方程;
(2)若直线AB的方向向量为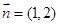 ,当焦点为
,当焦点为 时,求
时,求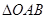 的面积;
的面积;
(3)若M是抛物线C准线上的点,求证:直线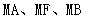 的斜率成等差数列.
的斜率成等差数列.
【答案】
(1) 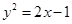 ;(2)
;(2) 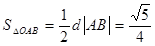 。
。
(3)显然直线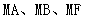 的斜率都存在,分别设为
的斜率都存在,分别设为 .
.
点 的坐标为
的坐标为 .
.
联立方程组得到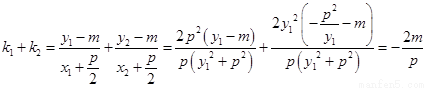 ,
,
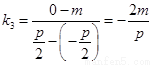 ,得到
,得到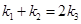 .
.
【解析】
试题分析:
思路分析:(1) 利用“代入法”。
(2) 联立方程组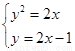 得,
得, ,应用弦长公式求
,应用弦长公式求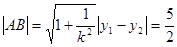
 ,得到面积。
,得到面积。
(3)直线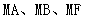 的斜率都存在,分别设为
的斜率都存在,分别设为 .
.
点 的坐标为
的坐标为 .
.
设直线AB: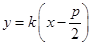 ,代入抛物线得
,代入抛物线得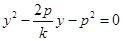 ,
确定
,
确定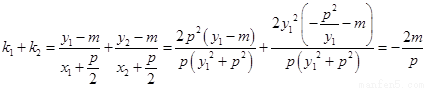 ,
,
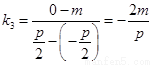 ,得到
,得到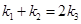 .
.
解:(1) 设 ,
,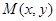 ,焦点
,焦点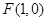 ,则由题意
,则由题意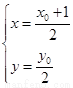 ,即
,即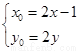
所求的轨迹方程为 ,即
,即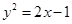
(2)  ,
, ,直线
,直线 ,
,
由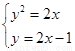 得,
得, ,
,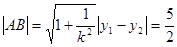
 ,
,
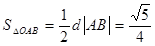 。
。
(3)显然直线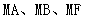 的斜率都存在,分别设为
的斜率都存在,分别设为 .
.
点 的坐标为
的坐标为 .
.
设直线AB: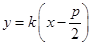 ,代入抛物线得
,代入抛物线得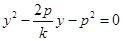 ,
所以
,
所以 ,
,
又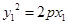 ,
, ,
,
因而 ,
,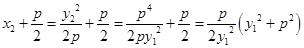
因而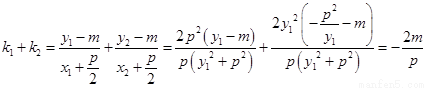
而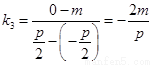 ,故
,故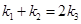 .
.
考点:等差数列,求轨迹方程,直线与抛物线的位置关系。
点评:中档题,涉及“弦中点”问题,往往利用“代入法”求轨迹方程。涉及直线与圆锥曲线的位置关系问题,往往通过联立方程组,应用韦达定理,简化解题过程。

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
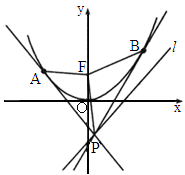
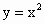 的焦点为F,动点P在直线l:x-y-2=0上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
的焦点为F,动点P在直线l:x-y-2=0上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.