题目内容
某精密配件厂准备生产甲、乙、丙三件不同的精密配件,制作过程都必须先后经过两次打磨,当第一次打磨合格后方可进入第二次打磨,两次打磨过程相互独立.据该厂现有的技术水平,经过一次打磨后,甲、乙、丙三件配件合格的概率依次为0.5,0.4,p;经过第二次打磨后,甲、乙、丙三件产品合格的概率依次为0.6,0.75,0.5.若第一次打磨后恰有一件产品合格的概率为0.38.(I)求p的值;
(Ⅱ)若经过前后两次打磨后,不合格配件的个数为ξ,求随机变量ξ的期望.
【答案】分析:(I)记甲、乙、丙经过第一次打磨后合格为事件A1、A2、A3.设E表示第一次打磨后恰有一件合格,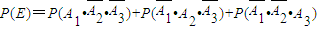 ,代入数据计算可得;(II)解法一:分别求ξ=0,1,2,3时的概率,由期望的定义可得;解法二:可得ξ~B(3,0.7),故Eξ=np,计算可得.
,代入数据计算可得;(II)解法一:分别求ξ=0,1,2,3时的概率,由期望的定义可得;解法二:可得ξ~B(3,0.7),故Eξ=np,计算可得.
解答:解:(I)分别记甲、乙、丙经过第一次打磨后合格为事件A1、A2、A3.
设E表示第一次打磨后恰有一件合格,则P(E)=0.38
∴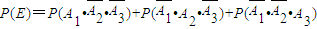 …(4分)
…(4分)
∴0.5×0.6×(1-p)+0.5×0.4×(1-p)+0.5×0.6×p=0.38,
解得p=0.6.…(6分)
(II)解法一:分别记甲、乙、丙经过两次打磨后合格为事件A、B、C
则P(A)=0.3,P(B)=0.3,P(C)=0.3…(8分)
∴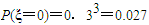 ,
,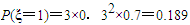 ,
,
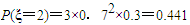 ,
,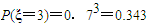 ,
,
∴Eξ=1×0.189+2×0.441+3×0.343=2.1.…(12分)
解法二:因为每件产品经过两次打磨后合格的概率均是0.3,…(8分)
即两次打磨后不合格的概率均为0.7…(10分)
故ξ~B(3,0.7),故Eξ=np=3×0.7=2.1…(12分)
点评:本题考查离散型随机变量的期望的求解,涉及相互独立事件的概率公式,属中档题.
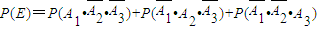 ,代入数据计算可得;(II)解法一:分别求ξ=0,1,2,3时的概率,由期望的定义可得;解法二:可得ξ~B(3,0.7),故Eξ=np,计算可得.
,代入数据计算可得;(II)解法一:分别求ξ=0,1,2,3时的概率,由期望的定义可得;解法二:可得ξ~B(3,0.7),故Eξ=np,计算可得.解答:解:(I)分别记甲、乙、丙经过第一次打磨后合格为事件A1、A2、A3.
设E表示第一次打磨后恰有一件合格,则P(E)=0.38
∴
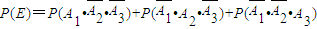 …(4分)
…(4分)∴0.5×0.6×(1-p)+0.5×0.4×(1-p)+0.5×0.6×p=0.38,
解得p=0.6.…(6分)
(II)解法一:分别记甲、乙、丙经过两次打磨后合格为事件A、B、C
则P(A)=0.3,P(B)=0.3,P(C)=0.3…(8分)
∴
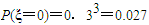 ,
,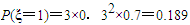 ,
,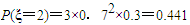 ,
,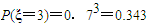 ,
,∴Eξ=1×0.189+2×0.441+3×0.343=2.1.…(12分)
解法二:因为每件产品经过两次打磨后合格的概率均是0.3,…(8分)
即两次打磨后不合格的概率均为0.7…(10分)
故ξ~B(3,0.7),故Eξ=np=3×0.7=2.1…(12分)
点评:本题考查离散型随机变量的期望的求解,涉及相互独立事件的概率公式,属中档题.

练习册系列答案
相关题目