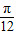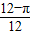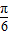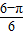题目内容
向一个边长分别为3，4，5的三角形内投一根针，则针尖不落在三角形的内切圆内的概率为（ ）
分析：先利用直角三角形三边与内切圆半径的关系求出半径，然后分别求出三角形和内切圆的面积，根据几何概型的概率公式即可求出所求．
解答：解：根据题意作出图形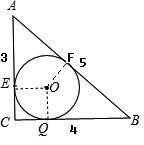
∵AC2+BC2=9+16=25，AB2=25，
∴AC2+BC2=AB2，
∴∠C=90°，
连接OE、OQ，
∵圆O是三角形ABC的内切圆，
∴AE=AF，BQ=BF，∠OEC=∠OQC=∠C=90°，OE=OQ，
∴四边形OECQ是正方形，
∴设OE=CE=CQ=OQ=r，
∵AF+BF=5，
∴3-r+4-r=5，
∴r=1，
∴三角形的内切圆的面积为π，三角形的面积为6
∴针尖不落在三角形的内切圆内的概率为1-
=
故选D．
∵AC2+BC2=9+16=25，AB2=25，
∴AC2+BC2=AB2，
∴∠C=90°，
连接OE、OQ，
∵圆O是三角形ABC的内切圆，
∴AE=AF，BQ=BF，∠OEC=∠OQC=∠C=90°，OE=OQ，
∴四边形OECQ是正方形，
∴设OE=CE=CQ=OQ=r，
∵AF+BF=5，
∴3-r+4-r=5，
∴r=1，
∴三角形的内切圆的面积为π，三角形的面积为6
∴针尖不落在三角形的内切圆内的概率为1-
| π |
| 6 |
| 6-π |
| 6 |
故选D．
点评：本题主要考查了直角三角形内切圆的有关知识，以及几何概型的概率公式，同时考查了推理能力和运算求解的能力，属于中档题．
练习册系列答案
相关题目
a与
a，高为b，向该矩形内随机投一点，则所投的点落在梯形内部的概率为___________.
