题目内容
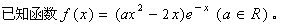
(1)当
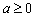 时,求
时,求 的极值点;
的极值点;(2)设
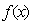 在[-1,1]上是单调函数,求出a的取值范围。
在[-1,1]上是单调函数,求出a的取值范围。 解:(1)令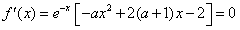 , ,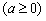 当a=0时,解得:x=1, ∵x<1,  <0;x>1, <0;x>1,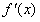 >0, >0, ∴x=1时,f(x)取得极小值, 当 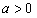 时, 时,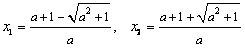 , ,易得: 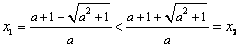 ,从而有下表 ,从而有下表
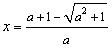 是函数的极小值点, 是函数的极小值点,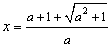 是函数的极大值点。 是函数的极大值点。(2)①当a=0时,由(1)可知,函数在[-1,1]上单减,符合题意; ②当 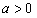 时,若函数在[-1,1]上单增, 时,若函数在[-1,1]上单增,则 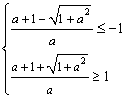 ,解得: ,解得: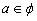 ; ;若函数在[-1,1]上单减,则 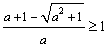 或 或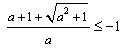 ,解得: ,解得: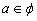 ; ;③ 当  时, 时,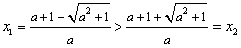 , ,若函数在[-1,1]上单增,则 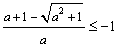 或 或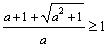 ,解得: ,解得: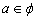 ; ;若函数在[-1,1]上单减,则 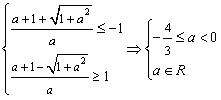 ,解得: ,解得: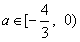 ; ;综上所述, 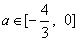 时,函数在[-1,1]上是单减函数。 时,函数在[-1,1]上是单减函数。 |

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
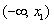
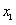
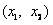
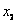
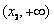
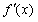
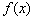
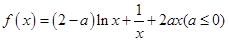 .
.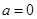 时,求
时,求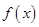 的极值;(2)当
的极值;(2)当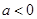 时,讨论
时,讨论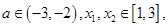 恒有
恒有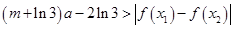 成立,求实数
成立,求实数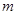 的取值范围.
的取值范围. 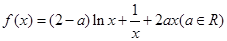
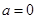 时,求
时,求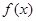 的极值
的极值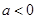 时,求
时,求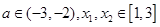 ,恒有
,恒有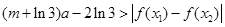 成立,求实数
成立,求实数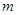 的取值范围。
的取值范围。 ,其中a为正实数。
,其中a为正实数。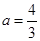 时,求
时,求 的极值点;
的极值点;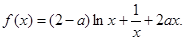
 时,求
时,求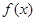 的极值;
的极值; 时,求
时,求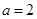 时,对任意的正整数
时,对任意的正整数 ,在区间
,在区间 上总有
上总有 个数使得
个数使得 成立,试求正整数
成立,试求正整数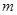 的最大值。
的最大值。
 时,求
时,求 的极值
的极值 时,求
时,求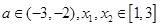 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围。
的取值范围。