题目内容
防疫站有A、B、C、D四名内科医生和E、F两名儿科医生,现将他们分成两个3人小组分别派往甲、乙两地指导疾病防控.两地都需要既有内科医生又有儿科医生,而且A只能去乙地.则不同的选派方案共有
- A.6种
- B.8种
- C.12种
- D.16种
A
分析:本题是一个分类计数问题,两地都需要既有内科医生又有儿科医生,表示两地至少有一个儿科医生和一个内科医生,分成三人小组可以直接分给甲组,有C21C32种结果,余下的分给乙,得到结果.
解答:由题意知本题是一个分类计数问题,
两地都需要既有内科医生又有儿科医生,表示两地至少有一个儿科医生和一个内科医生,
分成三人小组可以直接分给甲组,有C21C32=6种结果,
给甲分配以后余下的分给乙,
故选A.
点评:本题考查排列组合及计数原理,问题在解答过程中最主要的是看清条件中对于元素的限制,注意写出要做到不重不漏,本题是一个基础题.
分析:本题是一个分类计数问题,两地都需要既有内科医生又有儿科医生,表示两地至少有一个儿科医生和一个内科医生,分成三人小组可以直接分给甲组,有C21C32种结果,余下的分给乙,得到结果.
解答:由题意知本题是一个分类计数问题,
两地都需要既有内科医生又有儿科医生,表示两地至少有一个儿科医生和一个内科医生,
分成三人小组可以直接分给甲组,有C21C32=6种结果,
给甲分配以后余下的分给乙,
故选A.
点评:本题考查排列组合及计数原理,问题在解答过程中最主要的是看清条件中对于元素的限制,注意写出要做到不重不漏,本题是一个基础题.

练习册系列答案
相关题目
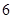 种 B.
种 B.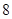 种 C.
种 C.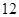 种 D.
种 D.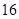 种
种