题目内容
(2009四川卷文)(本小题满分12分)
如图,正方形![]() 所在平面与平面四边形
所在平面与平面四边形![]() 所在平面互相垂直,△
所在平面互相垂直,△![]() 是等腰直角三角形,
是等腰直角三角形,![]()
(I)求证:![]() ;
;
(II)设线段![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() ,求证:
,求证: ![]() ∥
∥![]()
 (III)求二面角
(III)求二面角![]() 的大小。
的大小。
【解析】解法一:
因为平面ABEF⊥平面ABCD,BC![]() 平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
所以BC⊥平面ABEF.
所以BC⊥EF.
因为⊿ABE为等腰直角三角形,AB=AE,
所以∠AEB=45°,
又因为∠AEF=45,
所以∠FEB=90°,即EF⊥BE.
因为BC![]() 平面ABCD, BE
平面ABCD, BE![]() 平面BCE,
平面BCE,
BC∩BE=B
所以![]()
…………………………………………6分
(II)取BE的中点N,连结CN,MN,则MN![]()
![]()
![]() PC
PC
∴ PMNC为平行四边形,所以PM∥CN.
∵ CN在平面BCE内,PM不在平面BCE内,
∴ PM∥平面BCE. …………………………………………8分
(III)由EA⊥AB,平面ABEF⊥平面ABCD,易知EA⊥平面ABCD.
作FG⊥AB,交BA的延长线于G,则FG∥EA.从而FG⊥平面ABCD,
作GH⊥BD于H,连结FH,则由三垂线定理知BD⊥FH.
∴ ∠FHG为二面角F-BD-A的平面角.
∵ FA=FE,∠AEF=45°,
∠AEF=90°, ∠FAG=45°.
设AB=1,则AE=1,AF=![]() ,则
,则![]()
在Rt⊿BGH中, ∠GBH=45°,BG=AB+AG=1+![]() =
=![]() ,
,
![]() ,
,
在Rt⊿FGH中, ![]() ,
,
∴ 二面角![]() 的大小为
的大小为![]()
…………………………………………12分
解法二: 因![]() 等腰直角三角形,
等腰直角三角形,![]() ,所以
,所以![]()
|
所以![]()
即![]() 两两垂直;如图建立空间直角坐标系,
两两垂直;如图建立空间直角坐标系,
(I) 设![]() ,则
,则![]() ,
,![]()
∵![]() ,∴
,∴![]() ,
,
从而![]()
![]() ,
,![]()
于是![]() ,
,![]()
∴![]()
![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]()
∵![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
∴![]()
(II)![]() ,从而
,从而![]()
于是![]()
∴![]() ⊥
⊥![]() ,又
,又![]() ⊥平面
⊥平面![]() ,直线
,直线![]() 不在平面
不在平面![]() 内,
内,
故![]() ∥平面
∥平面![]()
(III)设平面![]() 的一个法向量为
的一个法向量为![]() ,并设
,并设![]() =(
=(![]()
![]()
 即
即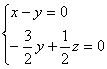
取![]() ,则
,则![]() ,
,![]() ,从而
,从而![]() =(1,1,3)
=(1,1,3)
取平面![]() D的一个法向量为
D的一个法向量为![]()
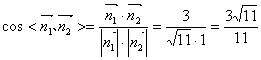
故二面角![]() 的大小为
的大小为![]()

 阅读快车系列答案
阅读快车系列答案(2009四川卷文)(本小题满分12分)
|
(I)求证:![]() ;
;
(II)设线段![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() ,
,
求证: ![]() ∥
∥![]()
(III)求二面角![]() 的大小。
的大小。


 ,
, ,
, ,
, 为实数,且
为实数,且