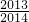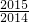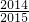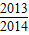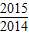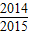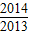Question

对于每个自然数n，一元二次函数y=（n²+n）x²-（2n+1）x+1与x轴交于A_n，B_n两点，以|A_nB_n|表示该两点间的距离，则|A₁B₁|+|A₂B₂|+…+|A₂₀₁₄B₂₀₁₄|的值是（　　）

• A．

  2013

  2014

• B．

  2015

  2014

• C．

  2014

  2015

• D．

  2014

  2013

Answer 1

分析：先确定A_n，B_n的坐标，代入两点间的距离公式可得到|A_nB_n|的关系式，然后代入，利用叠加法，即可求得结论．

解答：解：∵y=（n²+n）x²-（2n+1）x+1=（nx-1）[（n+1）x-1]，
∴由y=0得x=

1

n

或x=

1

n+1

∴A_n（

1

n+1

，0），B_n（

1

n

，0），
∴|A_nB_n|=

1

n

-

1

n+1

∴|A₁B₁|+|A₂B₂|+…+|A₂₀₁₄B₂₀₁₄|=1-

1

2

+

1

2

-

1

3

+…+

1

2014

-

1

2015

=1-

1

2015

=

2014

2015

故选C．

点评：本题考查数列与函数的综合，考查学生分析问题与转化求解的能力，属于中档题．