题目内容
在△ABC中,有命题:
①
-
=
;
②
+
+
=
;
③若(
+
)•(
-
)=0,则△ABC为等腰三角形;
④若
•
<0,则△ABC为钝角三角形.
上述命题正确的是( )
①
| AB |
| AC |
| BC |
②
| AB |
| BC |
| CA |
| 0 |
③若(
| AB |
| AC |
| AB |
| AC |
④若
| AC |
| AB |
上述命题正确的是( )
| A、①② | B、①④ | C、②③ | D、②③④ |
分析:对于①根据向量的减法法则进行判定,对于②封闭的图形,首尾相连的向量和为零向量,可判定真假,对于③化简可得AB=AC,可判定形状,对于④
•
<0,则角A为钝角,可判定真假.
| AC |
| AB |
解答:解:①
-
=
+
=
,故①不正确;
②首尾连接的向量的和为零向量,则
+
+
=
,故正确;
③若(
+
)•(
-
)=0,则AB=AC,从而△ABC为等腰三角形,故正确;
④若
•
<0,则角A为钝角,从而△ABC为钝角三角形,故正确.
故选D.
| AB |
| AC |
| CA |
| AB |
| CB |
②首尾连接的向量的和为零向量,则
| AB |
| BC |
| CA |
| 0 |
③若(
| AB |
| AC |
| AB |
| AC |
④若
| AC |
| AB |
故选D.
点评:本题主要考查了向量的加减运算和几何意义,以及向量的数量积等有关知识,属于基础题.

练习册系列答案
相关题目
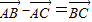 ;
;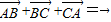 ;
;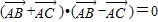 ,则△ABC为等腰三角形;
,则△ABC为等腰三角形;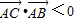 ,则△ABC为钝角三角形.
,则△ABC为钝角三角形.