题目内容
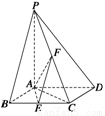
如图所示,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90°,
AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD.证明:
(1)PA⊥BD;
(2)平面PAD⊥平面PAB.
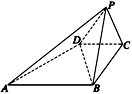
证明略
解析:
(1)取BC的中点O,
∵平面PBC⊥平面ABCD,△PBC为等边三角形,
∴PO⊥底面ABCD.
以BC的中点O为坐标原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,如图所示,建立空间直角坐标系.
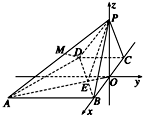
不妨设CD=1,则AB=BC=2,PO=![]() .
.
∴A(1,-2,0),B(1,0,0),D(-1,-1,0),P(0,0, ![]() ).
).
∴![]() =(-2,-1,0),
=(-2,-1,0),![]() =(1,-2,-
=(1,-2,- ![]() ).
).
∵![]() ·
·![]() =(-2)×1+(-1)×(-2)+0×(-
=(-2)×1+(-1)×(-2)+0×(-![]() )=0,
)=0,
∴![]() ⊥
⊥![]() ,∴PA⊥BD.
,∴PA⊥BD.
(2)取PA的中点M,连接DM,则M(![]() ,-1,
,-1,![]() ).
).
∵![]() =(
=(![]() ,0,
,0, ![]() ),
), ![]() =(1,0,-
=(1,0,-![]() ),
),
∴![]() ·
·![]() =
=![]() ×1+0×(-2)+
×1+0×(-2)+ ![]() ×(-
×(-![]() )=0,
)=0,
∴![]() ⊥
⊥![]() ,即DM⊥PA.
,即DM⊥PA.
又![]() ·
·![]() =
=![]() ×1+0×0+
×1+0×0+![]() ×(-
×(-![]() )=0,
)=0,
∴![]() ⊥
⊥![]() ,即DM⊥PB.
,即DM⊥PB.
又∵PA∩PB=P,∴DM⊥平面PAB,
∵DM![]() 平面PAD.
平面PAD.
∴平面PAD⊥平面PAB.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
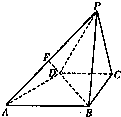 如图所示,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2,CD=1,侧面PBC⊥底面ABCD,点F在线段AP上,且满足
如图所示,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2,CD=1,侧面PBC⊥底面ABCD,点F在线段AP上,且满足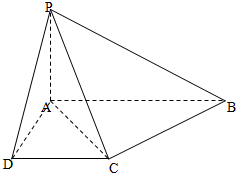 如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且
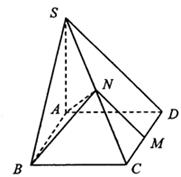
如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且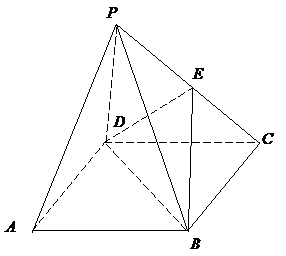
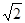 .
.
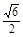 ,
,