Question

如图2-4-17,AB是⊙O的直径,PB切⊙O于点B,PA交⊙O于点C,∠APB的平分线分别交BC、AB于点D、E,交⊙O于点F,∠A=60°,并且线段AE、BD的长是一元二次方程x²-kx +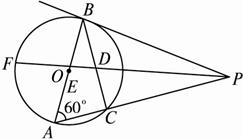=0的两个根(k为常数).

图2-4-17

(1)求证:PA·BD=PB·AE;

(2)证明⊙O的直径长为常数;

(3)求tan∠FPA的值.

Answer 1

思路分析:(1)由△PBD∽△PAE即可证得.?

(2)由韦达定理知AE +BD =k,只需证BE =BD,这可由角的相等证得.?

(3)要求tan∠FPA,先将∠FPA转化到直角三角形中,而∠FPB =∠FPA,∠FPB恰好在Rt△PBE中,解此三角形即可.

(1)证明:∵PB切⊙O于点B,∴∠PBD =∠A.?

又PE平分∠APB,∴∠APE =∠BPD.?

∴△PBD∽△PAE.∴=.?

∴PA·BD = PB·AE.

(2)解:由(1)知∠APE =∠EPB,?

又∵∠BED =∠A +∠EPA,∠BDE =∠PBC+∠EPB,?

∴∠BED =∠BDE.∴BE =BD.?

∵AE、BD为方程x²-kx +=0的两个根,?

∴AE +BD =k =AB.?

∴⊙O的直径为常数k.

(3)解:∵PB切⊙O于点B,AB为直径,?

∴∠PBA =90°.∵∠A =60°,?

∴PB =PA·sin60°=.?

由(1)得PA·BD =PB·AE,?

∴.?

∵AE、BD的长是方程x²-kx +=0的两个根,

∴AE·BD =.?

∴AE =2,BD =∴.?

在Rt△PBA中,PB =AB·tan60°=()·=.?

在Rt△PBE中,tan∠BPE = = =,?

又∠FPA =∠BPF,∴tan∠FPA =.