题目内容
若三角方程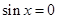
与
的解集分别为
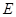和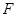
，则〖答〗（ ）
A．E?F B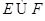 
C 
D D．E∩F=?
A
解析利用正弦函数的零点进行转化求解是解决本题的关键，注意整体思想的运用，结合集合的包含关系进行判断验证．解：由题意E={x|x=kπ，k∈Z}，由2x=kπ，得出x=kπ/2，k∈Z．故F={x|x==kπ/2，k∈Z}，?x∈E，可以得出x∈F，
反之不成立，故E是F的真子集，A符合．
故选A．
练习册系列答案
相关题目
若三角方程sinx=0 与sin2x=0 的解集分别为E，F，则（ ）
| A、E?F | B、E?F | C、E=F | D、E∩F=∅ |
与
的解集分别为
和
，则 （ ）
B．
C．
D．
与
的解集分别为
和
，则 （ ）
B．
C．
D．
与
的解集分别为
和
，则〖答〗 （ ）
B．
C．
D．