题目内容
一个数字生成器,生成规则如下:第1次生成一个数x,以后每次生成的结果是将上一次生成的每一个数x生成两个数,一个是-x,另一个是x+3.设第n次生成的数的个数为an,则数列{an}的前n项和Sn=分析:(1)根据题意,一个数字生成器,生成规则可得:第1次生成1个数,第二次生成2个数,第三次生成4个数,第四次生成8个数…,以此类推知该数列是等比数列,利用等比数列求和公式即可求出数列{an}的前n项和Sn
(2)因为一个数字生成器,生成规则如下:第1次生成一个数x,以后每次生成的结果是将上一次生成的每一个数x生成两个数,一个是-x,另一个是x+3,类推可求出数列的和.
(2)因为一个数字生成器,生成规则如下:第1次生成一个数x,以后每次生成的结果是将上一次生成的每一个数x生成两个数,一个是-x,另一个是x+3,类推可求出数列的和.
解答:解:(1)根据题意,一个数字生成器,生成规则可得:第1次生成1个数,第二次生成2个数,第三次生成4个数,第四次生成8个数…,以此类推,第n次生成的数的个数为an=2n-1,
显然,此数列为首项为1,公比为2的等比数列.再根据等比数列求和公式,则数列{an}的前n项和
Sn=2n-1.
(2)因为一个数字生成器,生成规则如下:第1次生成一个数x,以后每次生成的结果是将上一次生成的每一个数x生成两个数,一个是-x,另一个是x+3.
第一次生成的数为“1”,
第二次生成的数为“-1、4”,
第三次生成的数为“1、2、-4、7”,
第四次生成的数为“-1、4、-2、5、4、-1、-7、10”
…
可观察出:
第一次生成后前1次所有数中不同的个数为“1”,
第2次生成后前2次所有数中不同的个数为“3”,
第三次生成后前3次所有数中不同的个数为“6”,
第四次生成后前4次所有数中不同的个数为“10”,
…
以此类推以后为公差为4的等差数列.则易得数中不同的数的个数为Tn,则Tn=
所以,应填上Tn=
显然,此数列为首项为1,公比为2的等比数列.再根据等比数列求和公式,则数列{an}的前n项和
Sn=2n-1.
(2)因为一个数字生成器,生成规则如下:第1次生成一个数x,以后每次生成的结果是将上一次生成的每一个数x生成两个数,一个是-x,另一个是x+3.
第一次生成的数为“1”,
第二次生成的数为“-1、4”,
第三次生成的数为“1、2、-4、7”,
第四次生成的数为“-1、4、-2、5、4、-1、-7、10”
…
可观察出:
第一次生成后前1次所有数中不同的个数为“1”,
第2次生成后前2次所有数中不同的个数为“3”,
第三次生成后前3次所有数中不同的个数为“6”,
第四次生成后前4次所有数中不同的个数为“10”,
…
以此类推以后为公差为4的等差数列.则易得数中不同的数的个数为Tn,则Tn=
所以,应填上Tn=
|
点评:本题主要考查数列求和以及求数列递推式的知识点,主要利用不完全归纳法,不完全归纳法是解决数列问题的常用方法,尤其是在解决选择题和填空题上.要认真观察分析其特征,然后归纳出规律,并用通项的代数式表示,还要注意验证.

练习册系列答案
相关题目
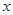 ,以后每次生成的结果是将上一次生成的每一个数
,以后每次生成的结果是将上一次生成的每一个数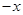 ,另一个是
,另一个是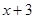 .设第
.设第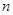 次生成的数的个数为
次生成的数的个数为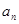 ,
,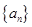 的前
的前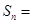 ;若
;若 ,前
,前 ,则
,则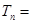 .
.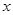 ,以后每次生成的结果可将上一次生成的每一个数
,以后每次生成的结果可将上一次生成的每一个数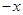 ,另一个是
,另一个是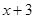 .设第
.设第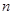 次生成的数的个数为
次生成的数的个数为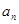 ,则数列
,则数列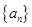 的前
的前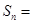 _________________;若
_________________;若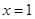 ,前
,前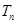 ,则
,则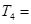 ______________________.
______________________.