题目内容
已知n∈N*,且(x+
)n展开式中前三项系数成等差数列.
(1)求n;
(2)求展开式中二项式系数最大的项;
(3)若(x+
)n=a0+a1(x-
)+a2(x-
)2+…+an(x-
)n,求a0+a1+…+an的值.
| 1 |
| 2 |
(1)求n;
(2)求展开式中二项式系数最大的项;
(3)若(x+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:(1)根据通项公式和题中条件求得
+(
)2
=2(
),由此解得n的值.
(2)由(1)知,二项式系数最大的值为
,为第五项,利用通项公式求得第五项.
(3)分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和.
| C | 0 n |
| 1 |
| 2 |
| C | 2 n |
| 1 |
| 2 |
| C | 1 n |
(2)由(1)知,二项式系数最大的值为
| C | 4 8 |
(3)分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和.
解答:解:(1)由于二项式的通项公式为Tr+1=
xn-r•(
)r=(
)r•
•xr,
则由题意得
+(
)2
=2(
),…(2分)
解得n=8.…(4分)
(2)由(1)知,二项式系数最大的值为
,为第五项.…(6分)
且 T5=
x4(
)4=
x4.…(8分)
(3)∵(x+
)8=[(x-
)+1]8=a0+a1(x-
)+a2(x-
)2+…+a8(x-
)8,…(9分)
令x=
,…(10分)
得a0+a1+…+a8=28=256.…(12分)
| C | r n |
| 1 |
| 2 |
| 1 |
| 2 |
| C | r n |
则由题意得
| C | 0 n |
| 1 |
| 2 |
| C | 2 n |
| 1 |
| 2 |
| C | 1 n |
解得n=8.…(4分)
(2)由(1)知,二项式系数最大的值为
| C | 4 8 |
且 T5=
| C | 4 8 |
| 1 |
| 2 |
| 35 |
| 8 |
(3)∵(x+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
令x=
| 3 |
| 2 |
得a0+a1+…+a8=28=256.…(12分)
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
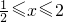 }且M∩P≠∅求实数a的取值范围;
}且M∩P≠∅求实数a的取值范围; }且M∩P≠∅求实数a的取值范围;
}且M∩P≠∅求实数a的取值范围; }且M∩P≠∅求实数a的取值范围;
}且M∩P≠∅求实数a的取值范围; }且M∩P≠∅求实数a的取值范围;
}且M∩P≠∅求实数a的取值范围;