题目内容
P是△ABC内的一点 =
= (
( +
+ ),则△ABC的面积与△ABP 的面积之比为
),则△ABC的面积与△ABP 的面积之比为
- A.2
- B.3
- C.3/2
- D.6
B
分析:设 (
( +
+ )=
)= ,则D是BC的中点,由
,则D是BC的中点,由 =
= (
( +
+ ),知
),知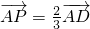 ,设△ABC在AB边上的高为h,则△ABP在AB边上的高为
,设△ABC在AB边上的高为h,则△ABP在AB边上的高为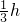 ,由此能求出△ABC的面积与△ABP的面积之比.
,由此能求出△ABC的面积与△ABP的面积之比.
解答: 解:设
解:设 (
( +
+ )=
)= ,则D是BC的中点,
,则D是BC的中点,
∵ =
= (
( +
+ ),
),
∴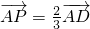 ,
,
如图,过D作DE∥AB,交AC于E,过P作MN∥AB,交AC于N,交BC于M,
设△ABC在AB边上的高为h,则△ABP在AB边上的高为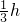 ,
,
∴△ABC的面积与△ABP的面积之比= =3.
=3.
故选B.
点评:三角形面积性质:同(等)底同(等)高的三角形面积相等;同(等)底三角形面积这比等于高之比;同(等)高三角形面积之比等于底之比.
分析:设
 (
( +
+ )=
)= ,则D是BC的中点,由
,则D是BC的中点,由 =
= (
( +
+ ),知
),知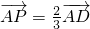 ,设△ABC在AB边上的高为h,则△ABP在AB边上的高为
,设△ABC在AB边上的高为h,则△ABP在AB边上的高为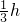 ,由此能求出△ABC的面积与△ABP的面积之比.
,由此能求出△ABC的面积与△ABP的面积之比.解答:
 解:设
解:设 (
( +
+ )=
)= ,则D是BC的中点,
,则D是BC的中点,∵
 =
= (
( +
+ ),
),∴
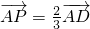 ,
,如图,过D作DE∥AB,交AC于E,过P作MN∥AB,交AC于N,交BC于M,
设△ABC在AB边上的高为h,则△ABP在AB边上的高为
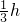 ,
,∴△ABC的面积与△ABP的面积之比=
 =3.
=3.故选B.
点评:三角形面积性质:同(等)底同(等)高的三角形面积相等;同(等)底三角形面积这比等于高之比;同(等)高三角形面积之比等于底之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.
(1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.