题目内容
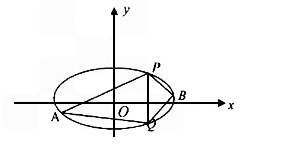
已知椭圆C的中心在原点,焦点在x轴上,离心率等于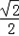 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线
y2=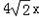 的焦点.PQ过椭圆焦点且PQ⊥x轴,A、B是椭圆位于直线PQ两侧的两动点.
的焦点.PQ过椭圆焦点且PQ⊥x轴,A、B是椭圆位于直线PQ两侧的两动点.
(1)求椭圆C的方程;
(2)若直线AB的斜率为1,求四边形APBQ面积的最大值;
(3)当A、B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
解 设椭圆C的方程为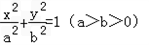
∵椭圆的一个顶点恰好是抛物线y2= 的焦点,
的焦点,
∴a= ∵离心率等于
∵离心率等于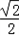 ,
,
∴ ,∴c=1∴b=1
,∴c=1∴b=1
∴椭圆C的方程为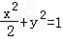 ;
;
(2)设A(x1,y1),B(x2,y2),直线AB的方程为y=x+t,代入椭圆方程,
消元可得3x2+4tx+2t2﹣2=0由△>0,解得﹣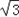 <t<
<t<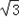
由韦达定理得x1+x2=﹣ t,x1x2=
t,x1x2= .
.
∵PQ过椭圆焦点且PQ⊥x轴,∴|PQ|=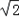
∴四边形APBQ的面积S= ×
×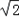 ×|x1﹣x2|=
×|x1﹣x2|= ×
×
∴t=0时,Smax=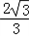 ;
;
(3)当∠APQ=∠BPQ,则PA、PB的斜率之和为0,
设直线PA的斜率为k,则PB的斜率为﹣k,PA的直线方程为y﹣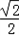 =k(x﹣1),
=k(x﹣1),
与椭圆方程联立,消元可得(1+2k2)x2+(2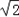 k﹣4k2)x+k2﹣2
k﹣4k2)x+k2﹣2 k﹣1=0
k﹣1=0
∴x1+1=﹣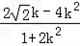 同理x2+1=﹣
同理x2+1=﹣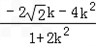
∴x1+x2=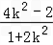 ,x1﹣x2=﹣
,x1﹣x2=﹣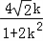
∴y1﹣y2=k(x1+x2)﹣2k=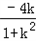 ,x1﹣x2=﹣
,x1﹣x2=﹣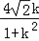
∴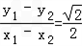
∴直线AB的斜率为定值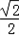 .
.
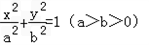
∵椭圆的一个顶点恰好是抛物线y2=
 的焦点,
的焦点,∴a=
 ∵离心率等于
∵离心率等于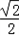 ,
,∴
 ,∴c=1∴b=1
,∴c=1∴b=1∴椭圆C的方程为
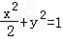 ;
;(2)设A(x1,y1),B(x2,y2),直线AB的方程为y=x+t,代入椭圆方程,
消元可得3x2+4tx+2t2﹣2=0由△>0,解得﹣
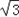 <t<
<t<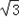
由韦达定理得x1+x2=﹣
 t,x1x2=
t,x1x2= .
.∵PQ过椭圆焦点且PQ⊥x轴,∴|PQ|=
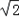
∴四边形APBQ的面积S=
 ×
×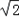 ×|x1﹣x2|=
×|x1﹣x2|= ×
×
∴t=0时,Smax=
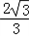 ;
;(3)当∠APQ=∠BPQ,则PA、PB的斜率之和为0,
设直线PA的斜率为k,则PB的斜率为﹣k,PA的直线方程为y﹣
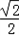 =k(x﹣1),
=k(x﹣1),与椭圆方程联立,消元可得(1+2k2)x2+(2
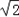 k﹣4k2)x+k2﹣2
k﹣4k2)x+k2﹣2 k﹣1=0
k﹣1=0∴x1+1=﹣
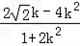 同理x2+1=﹣
同理x2+1=﹣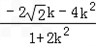
∴x1+x2=
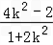 ,x1﹣x2=﹣
,x1﹣x2=﹣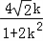
∴y1﹣y2=k(x1+x2)﹣2k=
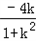 ,x1﹣x2=﹣
,x1﹣x2=﹣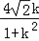
∴
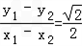
∴直线AB的斜率为定值
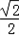 .
.
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目

 。
。