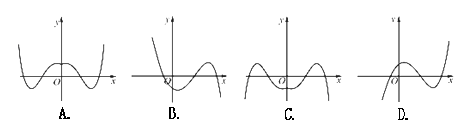
题目内容
已知偶函数 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减,且满足
上单调递减,且满足 ,则不等式
,则不等式 的解集是( )
的解集是( )
A. | B. |
C. | D. |
D
解析试题分析:由题意可知,函数 在
在 ,
,
且 ,∵
,∵ ,∴
,∴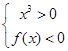 或
或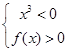 ,
,
即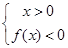 或
或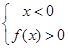 ,∴
,∴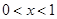 或
或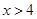 或
或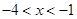 .
.
考点:1.偶函数;2.函数单调性;3.函数图像.

练习册系列答案
相关题目
某社区要召开群众代表大会,规定各小区每10人推选一名代表,当各小区人数除以10的余数不小于5时再增选一名代表.那么,各小区可推选代表人数y与该小区人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为 ( )
A.y=[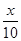 ] ] | B.y=[ ] ] | C.y=[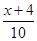 ] ] | D.y=[ ] ] |
已知函数 ,
, 满足
满足 ,且
,且 在
在 上的导数满足
上的导数满足 ,则不等式
,则不等式 的解为( )
的解为( )
A. | B. |
C.   | D. |
函数 ,则该函数为( )
,则该函数为( )
| A.单调递增函数,奇函数 | B.单调递增函数,偶函数 |
| C.单调递减函数,奇函数 | D.单调递减函数,偶函数 |
下列四个函数中,在区间 上是减函数的是( )
上是减函数的是( )
A. | B. | C. | D. |
函数 的定义域是( )
的定义域是( )
| A.(-1,1) | B. | C. | D.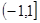 |
设方程 的两个根为
的两个根为 ,则( )
,则( )
A. | B. | C. | D. |
下列函数中,为奇函数的是( )
A. | B. | C. | D. |
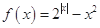 的图像为
的图像为