题目内容
已知函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,函数
上是增函数,函数![]() 在
在![]() 上有三个零点,且1是其中一个零点.
上有三个零点,且1是其中一个零点.
(1)求![]() 的值;
的值;
(2)求![]() 的取值范围;
的取值范围;
(3)试探究直线![]() 与函数
与函数![]() 的图像交点个数的情况,并说明理由.
的图像交点个数的情况,并说明理由.
(1)0(2)![]() (3)见解析
(3)见解析
解析:
(1)解:∵![]() ,∴
,∴![]() .
.
∵![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
∴当![]() 时,
时,![]() 取到极小值,即
取到极小值,即![]() .
.
∴![]() .
.
(2)解:由(1)知,![]() ,
,
∵1是函数![]() 的一个零点,即
的一个零点,即![]() ,∴
,∴![]() .
.
∵![]() 的两个根分别为
的两个根分别为![]() ,
,![]() .
.
∵![]() 在
在![]() 上是增函数,且函数
上是增函数,且函数![]() 在
在![]() 上有三个零点,
上有三个零点,
∴![]() ,即
,即![]() .∴
.∴![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.
(3)解:由(2)知![]() ,且
,且![]() .
.
要讨论直线![]() 与函数
与函数![]() 图像的交点个数情况,
图像的交点个数情况,
即求方程组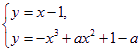 解的个数情况.
解的个数情况.
由![]() ,得
,得![]() .
.
即![]() .
.
即![]() .
.
∴![]() 或
或![]() .
.
由方程![]() , (*)
, (*)
得![]() .
.
∵![]() ,
,
若![]() ,即
,即![]() ,解得
,解得![]() .此时方程(*)无实数解.
.此时方程(*)无实数解.
若![]() ,即
,即![]() ,解得
,解得![]() .此时方程(*)有一个实数解
.此时方程(*)有一个实数解![]() .
.
若![]() ,即
,即![]() ,解得
,解得![]() .此时方程(*)有两个实数解,分别为
.此时方程(*)有两个实数解,分别为![]() ,
,![]() .
.
且当![]() 时,
时,![]() ,
,![]() .
.
综上所述,当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图像有一个交点.
的图像有一个交点.
当![]() 或
或![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图像有二个交点.
的图像有二个交点.
当![]() 且
且![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图像有三个交点.
的图像有三个交点.

练习册系列答案
相关题目
 的定义域为
的定义域为 ,部分对应值如下表,
,部分对应值如下表, 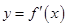 的图象如图所示.下列关于
的图象如图所示.下列关于

 ,
, ;
; 上是减函数;
上是减函数; 时,
时, 的最大值为4;
的最大值为4; 时,函数
时,函数 有
有 在
在 上是减函数,则
上是减函数,则 与
与 的大小关系为( )
的大小关系为( ) B.
B.
 D.无法比较大小
D.无法比较大小