题目内容
已知曲线C1: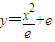 (e为自然对数的底数),曲线C2:y=2elnx和直线l:y=2x.
(e为自然对数的底数),曲线C2:y=2elnx和直线l:y=2x.(1)求证:直线l与曲线C1,C2都相切,且切于同一点;
(2)设直线x=t(t>0)与曲线C1,C2及直线l分别相交于M,N,P,记f(t)=|PM|-|NP|,求f(t)在[e-3,e3]上的最大值;
(3)设直线x=em(m=0,1,2,3┅┅)与曲线C1和C2的交点分别为Am和Bm,问是否存在正整数n,使得AB=AnBn?若存在,求出n;若不存在,请说明理由. (本小题参考数据e≈2.7).
【答案】分析:(1)欲证明:直线l与曲线C1,C2都相切,且切于同一点,只须根据切线的斜率分别求出切点的坐标即可,故先利用导数求出在切点处的导函数值,再结合导数的几何意义即可求出切线的斜率,最后利用斜率为2即可求出两个切点坐标.从而问题解决.
(2)先利用线段的长度表示出函数f(t),再利用导数研究函数的单调性,求出f(t)的导数,根据f′(t)>0求得的区间是单调增区间,最后求出最大值即可;
(3)对于存在性问题,可先假设存在,即假设存在正整数n,使得AB=AnBn,再设AnBn为g(n),利用导数研究函数g(n)的单调性,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(1)证明: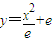
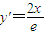 由
由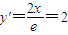 得x=e(2分)
得x=e(2分)
在C1上点(e,2e)处的切线为y-2e=2(x-e),即y=2x(3分)
又在C2上点(e,2e)处切线可计算得y-2e=2(x-e),即y=2x
∴直线l与C1、C2都相切,且切于同一点(e,2e)(4分)
(2)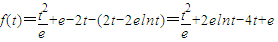
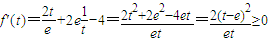 (6分)
(6分)
∴f(t)在[e-3,e3]上递增
∴当t=e3时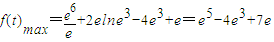 (8分)
(8分)
(3)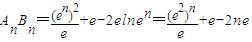
设上式为g(n),假设n取正实数,则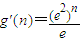 •
•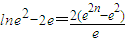
当n∈(0,1)时,g′(n)<0,∴g(n)递减;
当n∈(1,+∞),g′(n)>0,∴g(n)递增.(12分)
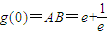 g(1)=2e-2e=0
g(1)=2e-2e=0
∴不存在正整数n,使得g(m)=g(0)
即AnBn=AB.(14分)
点评:本小题主要考查利用导数研究函数的单调性、利用导数求闭区间上函数的最值、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.
(2)先利用线段的长度表示出函数f(t),再利用导数研究函数的单调性,求出f(t)的导数,根据f′(t)>0求得的区间是单调增区间,最后求出最大值即可;
(3)对于存在性问题,可先假设存在,即假设存在正整数n,使得AB=AnBn,再设AnBn为g(n),利用导数研究函数g(n)的单调性,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(1)证明:
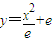
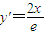 由
由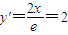 得x=e(2分)
得x=e(2分)在C1上点(e,2e)处的切线为y-2e=2(x-e),即y=2x(3分)
又在C2上点(e,2e)处切线可计算得y-2e=2(x-e),即y=2x
∴直线l与C1、C2都相切,且切于同一点(e,2e)(4分)
(2)
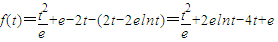
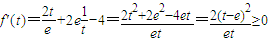 (6分)
(6分)∴f(t)在[e-3,e3]上递增
∴当t=e3时
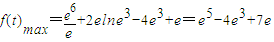 (8分)
(8分)(3)
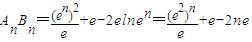
设上式为g(n),假设n取正实数,则
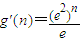 •
•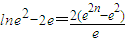
当n∈(0,1)时,g′(n)<0,∴g(n)递减;
当n∈(1,+∞),g′(n)>0,∴g(n)递增.(12分)
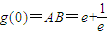 g(1)=2e-2e=0
g(1)=2e-2e=0
∴不存在正整数n,使得g(m)=g(0)
即AnBn=AB.(14分)
点评:本小题主要考查利用导数研究函数的单调性、利用导数求闭区间上函数的最值、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
相关题目
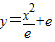 (e为自然对数的底数),曲线C2:y=2elnx和直线l:y=2x.
(e为自然对数的底数),曲线C2:y=2elnx和直线l:y=2x.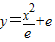 (e为自然对数的底数),曲线C2:y=2elnx和直线l:y=2x.
(e为自然对数的底数),曲线C2:y=2elnx和直线l:y=2x.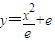 (e为自然对数的底数),曲线C2:y=2elnx和直线l:y=2x.
(e为自然对数的底数),曲线C2:y=2elnx和直线l:y=2x.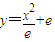 (e为自然对数的底数),曲线C2:y=2elnx和直线l:y=2x.
(e为自然对数的底数),曲线C2:y=2elnx和直线l:y=2x.