题目内容
已知动点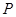 与双曲线
与双曲线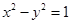 的两个焦点
的两个焦点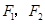 的距离之和为定值,且
的距离之和为定值,且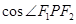 的最小值为
的最小值为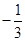 ,求动点
,求动点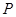 的轨迹方程.
的轨迹方程.
【答案】
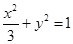 .
.
【解析】
试题分析: 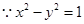 ,
,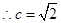 .
.
设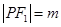 ,
, ,则
,则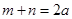 (常数
(常数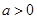 ),所以点
),所以点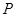 是以
是以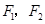 为焦点,
为焦点,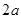 为长轴的椭圆,
为长轴的椭圆,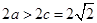 ,
,
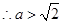 .
.
由余弦定理,有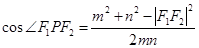
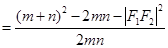
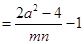 .
.
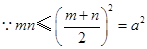 ,
,
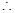 当且仅当
当且仅当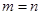 时,
时,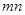 取得最大值
取得最大值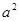 .
.
此时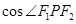 取得最小值
取得最小值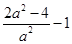 ,
,
由题意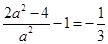 ,解得
,解得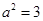 ,
,
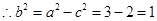 .
.
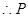 点的轨迹方程为
点的轨迹方程为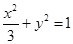 .
.
考点:本题主要考查椭圆、双曲线的定义及几何性质、余弦定理。
点评:利用椭圆定义,首先明确了所求轨迹为椭圆,利用双曲线的定义及几何性质,结合“焦点三角形”,运用余弦定理。是一道好题。

练习册系列答案
相关题目
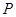 与双曲线
与双曲线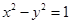 的两个焦点
的两个焦点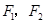 的距离之和为定值,且
的距离之和为定值,且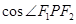 的最小值为
的最小值为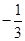 ,求动点
,求动点