题目内容

已知a>0，函数f（x）=x³-ax在［1，+∞）上是单调增函数，则a的最大值是

D
解：因为f′（x）=3x²-a，
∵函数f（x）=x³-ax在[1，+∞）上是单调增函数，
∴在[1，+∞）上，f′（x）≥0恒成立，
即a≤3x²在[1，+∞）上恒成立，
∴a≤3，
故答案为：3．

练习册系列答案

黄冈金牌之路中考精英总复习系列答案

相关题目

.(本小题满分12分）

已知函數f(x)=ln+mx2(m∈R)

(I)求函数f(x)的单调区间；

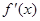(II)若m=0，A(a,f(a))、B(b，f(b))是函数f(x)图象上不同的两点，且a>b>0, 为f(x)的导函数，求证：

(III)求证

已知函数f(x)＝loga(ax－1)(a>0且a≠1)

(1)求f(x)的定义域；

(2)讨论f(x)的单调性；

(3)x为何值时，函数值大于1.

已知函数f(x)＝a－是偶函数，a为实常数.

(1)求b的值；

(2)当a＝1时，是否存在n>m>0，使得函数y＝f(x)在区间[m，n]上的函数值组成的集合也是[m，n]，若存在，求出m，n的值，否则，说明理由.

(3)若在函数定义域内总存在区间[m，n](m<n)，使得y＝f(x)在区间[m，n]上的函数值组成的集合也是[m，n]，求实数a的取值范围.

已知指函数ƒ(x)=a^x(a>0，且a≠1)自变量与函数值的部分对应值如右表：

那么a=_____；若函数y=x[ƒ(x)－2]，则满足条件y>0的x的集合为___________________.

x	-1	0	2
ƒ(x)	2	1	0.25

已知a>0，函数f（x）=x3-ax在［1，+∞）上是单调增函数，则a的最大值是