Question

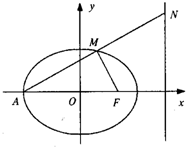如图，椭圆C：

x2

36

+

y2

20

=1的左顶点，右焦点分别为A，F，直线l的方程x=9，N为l上位于x轴上方的一点．
（1）设线段AN与椭圆C交于点M，且点M是线段AN的中点，求证：MA⊥MF；
（2）过三点A，F，N的圆与y轴交于P，Q两点，求线段PQ的长的取值范围．

Answer 1

分析：（1）首先求出A，F的坐标，并根据条件设设N（9，t），进而表示出M点坐标并代入椭圆方程求出M、N的坐标，再表示出向量MA与MF的积

MA

•

MF

=

15

2

•(-

5

2

) +

5 3

2

•

5 3

2

=0从而得出结论．
（2）设圆方程为x²+y²+Dx+Ey+F=0，并把A，F，N代入列出方程并解方程求出D、E、F，得到圆方程为x²+y²+2x-

t2+75

t

y-24=0，然后令x=0得到关于x、y的一元二次方程利用韦达定理表示出PQ并利用均值不等式即可求出结果．

解答：解：（1）由题意知a=6，b=2

5

，c=4
∴A（-6，0），F（4，0）
设N（9，t）（t＞0），则M（

3

2

，

t

2

）
∵M在椭圆上，∴

9 4

36

+

t2 4

20

=1
∵t＞0∴t=5

3

，则N（9，5

3

）
∴M（

3

2

，

5 3

2

）

MA

=(

15

2

，

5 3

2

)，

MF

=(-

5

2

，

5 3

2

)
∵

MA

•

MF

=

15

2

•(-

5

2

) +

5 3

2

•

5 3

2

=0
∴MA⊥MF
（2）设点A、F、N的圆方程为x²+y²+Dx+Ey+F=0
把A、F、N三点的坐标代入上式，得
36-6D+F=0   ①
16+4D+F=0 ②
81+t²+9D+Et+F=0  ③
联立①②③得，
D=2，F=-24
E=-

t2+75

t

则圆的方程为：x²+y²+2x-

t2+75

t

y-24=0
令x=0．得y²-

t2+75

t

y-24=0
∴PQ=|y1-y2|=

(t+ 75 t )2+96

≥

(2 t• 75 t )2+96

=6

11

当且仅当t=

75

t

即t=5

3

时，PQ取得最小值．
则PQ的长的取值范围是[6

11

，+∞）

点评：本题考查了直线与圆锥曲线的综合问题以及向量的运用，在圆锥曲线中灵活运用向量的知识，会使问题简单化，对于最值和取值范围的问题均值不等式是常用方法，但要注意均值不等式的条件．