Question

已知约束条件

x-3y+4≥0 x+2y-1≥0 3x+y-8≤0

若目标函数z=x+ay（a≥0）恰好在点（2，2）处取得最大值，则a的取值范围为（　　）

• A、0＜a＜

  1

  3

• B、a≥

  1

  3

• C、a＞

  1

  3

• D、0＜a＜

  1

  2

Answer 1

分析：先根据约束条件画出可行域，再利用几何意义求最值的方法，利用直线斜率之间的关系，只需求出直线z=x+ay的斜率的取值范围即可．

解答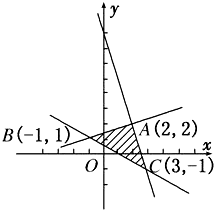：解：画出已知约束条件的可行域为△ABC内部（包括边界），
如图，易知当a=0时，不符合题意；
当a＞0时，由目标函数z=x+ay得y=-

1

a

x+

z

a

，
则由题意得-3=k_AC＜-

1

a

＜0，故a＞

1

3

．
综上所述，a＞

1

3

．
故选C．

点评：本题主要考查了简单的线性规划，以及利用几何意义求最值，属于基础题．由于线性规划的介入，借助于平面区域，可以研究函数的最值或最优解；借助于平面区域特性，我们还可以优化数学解题，借助于规划思想，巧妙应用平面区域，为我们的数学解题增添了活力．