题目内容
下列三个命题:①若函数f(x)=sin(2x+φ)的图象关于y轴对称,则φ=
| π |
| 2 |
②若函数f(x)=
| ax-2 |
| x-1 |
③函数f(x)=|x|+|x-2|的图象关于直线x=1对称.
其中真命题的序号是
分析:①根据三角函数图象的性质判断.
②根据函数的图象特征计算a的值,再做判断.
③根据函数图象的性质判断.
②根据函数的图象特征计算a的值,再做判断.
③根据函数图象的性质判断.
解答:解:①∵函数f(x)=sin(2x+φ)的图象关于y轴对称,
∴φ=
,
故命题为假.
②令g(x)=f(x+1)-1,
∵函数f(x)=
=的图象关于点(1,1)对称,
∴g(x)关于点(0,0)对称,
∴g(-x)=-g(x),
∴a=1.
胡命题为真.
③∵f(1-x)=f(1+x),
∴f(x)的图象关于直线x=1对称.
故命题为真.
故答案为②③.
∴φ=
| π |
| 8 |
故命题为假.
②令g(x)=f(x+1)-1,
∵函数f(x)=
| ax-2 |
| x-1 |
∴g(x)关于点(0,0)对称,
∴g(-x)=-g(x),
∴a=1.
胡命题为真.
③∵f(1-x)=f(1+x),
∴f(x)的图象关于直线x=1对称.
故命题为真.
故答案为②③.
点评:本题主要考查了命题真假的判断,同时要求熟练掌握函数图象的性质.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
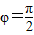 ;
; 的图象关于点(1,1)对称,则a=1;
的图象关于点(1,1)对称,则a=1;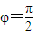 ;
;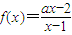 的图象关于点(1,1)对称,则a=1;
的图象关于点(1,1)对称,则a=1;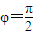 ;
;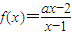 的图象关于点(1,1)对称,则a=1;
的图象关于点(1,1)对称,则a=1;