题目内容
三棱锥S—ABC中,SA⊥底面ABC,SA=4,AB=3,D为AB的中点,∠ABC=90°,则点D到面SBC的距离等于 ( )
A.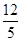 | B. | C.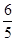 | D.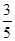 |
C
专题:计算题.
分析:先由面面垂直的性质找出点D到面SBC的距离DE,再利用三角形相似,对应边成比例求出DE的值.
解答:解:∵SA⊥底面ABC,SA=4,AB=3,D为AB的中点,∠ABC=90°,
∴BC⊥面SAB∴面 SBC⊥面SAB,在面SAB中,作DE⊥SB,
则 DE⊥面SBC,DE为所求.
由△BDE∽△BSA 得:DE :SA ="BD" :BS 即DE :4 =
 : 5 ,
: 5 ,∴DE=
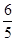 ,应选C。
,应选C。点评:本题考查线面垂直、面面垂直性质的应用.

练习册系列答案
相关题目
 -
- 中,点
中,点 到平面
到平面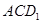 的距离 。
的距离 。
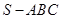 中,
中,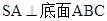 ,
,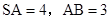 , D为AB的中点,∠ABC=90°,则点D到面SBC的距离等于
, D为AB的中点,∠ABC=90°,则点D到面SBC的距离等于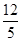
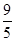
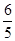

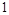 的正方体
的正方体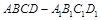 中,平面
中,平面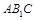 与平面
与平面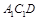 间的距离是( )
间的距离是( )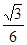
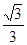
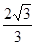
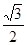
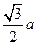 ,类比上述结论,在边长
,类比上述结论,在边长 为a的正四面体内任一点到其四个面的距离之和为定值 。
为a的正四面体内任一点到其四个面的距离之和为定值 。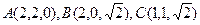 ,则坐标原点
,则坐标原点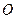 到平面
到平面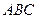
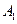
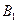
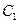
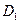 的棱上到异面直线AB,C
的棱上到异面直线AB,C
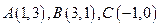 ,则
,则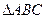 的面积是____________
的面积是____________