题目内容
【题目】如图,已知圆![]() 与
与![]() 轴交于
轴交于![]() 两点(
两点(![]() 在
在![]() 的上方),直线
的上方),直线![]() .
.

(1)当![]() 时,求直线
时,求直线![]() 被圆
被圆![]() 截得的弦长;
截得的弦长;
(2)若![]() ,点
,点![]() 为直线
为直线![]() 上一动点(不在
上一动点(不在![]() 轴上),直线
轴上),直线![]() 的斜率分别为
的斜率分别为![]() ,直线
,直线![]() 与圆的另一交点分别
与圆的另一交点分别![]() .
.
①问是否存在实数![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
②证明:直线![]() 经过定点,并求出定点坐标.
经过定点,并求出定点坐标.
【答案】(1)![]() (2)①存在
(2)①存在![]() 的值为
的值为![]() ;②见证明
;②见证明
【解析】
(1)利用点到直线的距离和勾股定理可得;(2)①利用斜率公式求得k1,k2,代入等式k1=mk2,可解得;②联立直线CB与圆O解得P的坐标,同理可得Q坐标,再根据斜率公式求得PQ的斜率,然后利用点斜式求得直线PQ方程,可得定点.
(1)当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,
,
圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以,直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ;
;
(2)若![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
①设![]() ,则
,则![]() ,
,![]() ,
,
由![]() 可得
可得![]() ,所以存在
,所以存在![]() 的值为
的值为![]() ;
;
②证明:直线![]() 方程为
方程为![]() ,与圆方程联立得:
,与圆方程联立得:![]() ,
,
所以,![]() ,解得
,解得![]() 或
或![]() ,
,
所以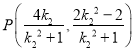 ,
,
同理可得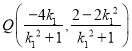 ,即
,即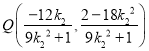
所以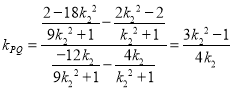
所以直线![]() 的方程为
的方程为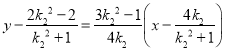 ,
,
即![]() ,所以,直线
,所以,直线![]() 经过定点
经过定点![]() .
.

练习册系列答案
相关题目
【题目】某机构为了调查某市同时符合条件![]() 与
与![]() (条件
(条件![]() :营养均衡,作息规律;条件
:营养均衡,作息规律;条件![]() :经常锻炼,劳逸结合)的高中男生的体重
:经常锻炼,劳逸结合)的高中男生的体重![]() (单位:
(单位:![]() )与身高
)与身高![]() (单位:
(单位: ![]() )是否存在较好的线性关系,该机构搜集了
)是否存在较好的线性关系,该机构搜集了![]() 位满足条件的高中男生的数据,得到如下表格:
位满足条件的高中男生的数据,得到如下表格:
身高/ |
|
|
|
|
|
|
体重/ |
|
|
|
|
|
|
根据表中数据计算得到![]() 关于
关于![]() 的线性回归方程对应的直线的斜率为
的线性回归方程对应的直线的斜率为![]() .
.
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到整数部分);
精确到整数部分);
(2)已知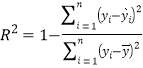 ,且当
,且当![]() 时,回归方程的拟合效果较好。试结合数据
时,回归方程的拟合效果较好。试结合数据![]() ,判断(1)中的回归方程的拟合效果是否良好?
,判断(1)中的回归方程的拟合效果是否良好?
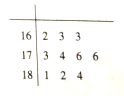
(3)该市某高中有![]() 位男生同时符合条件
位男生同时符合条件![]() 与
与![]() ,将这
,将这![]() 位男生的身高(单位:
位男生的身高(单位:![]() )的数据绘制成如下的茎叶图。利用(1)中的回归方程估计这
)的数据绘制成如下的茎叶图。利用(1)中的回归方程估计这![]() 位男生的体重未超过
位男生的体重未超过![]() 的所有男生体重(单位:
的所有男生体重(单位:![]() )的平均数(结果精确到整数部分).
)的平均数(结果精确到整数部分).