题目内容
已知奇函数f(x)是定义在(-3,3)上的减函数,且满足不等式f(x-3)+f(x2-3)<0,设不等式解集为A,B=A∪{x|1≤x≤![]() },求函数g(x)=-3x2+3x-4(x∈B)的最大值.
},求函数g(x)=-3x2+3x-4(x∈B)的最大值.
g(x)max=g(1)=-4.
解析:
由![]() 且x≠0,故0<x<
且x≠0,故0<x<![]() ,
,
又∵f(x)是奇函数,∴f(x-3)<-f(x2-3)=f(3-x2),又f(x)在(-3,3)上是减函数,
∴x-3>3-x2,即x2+x-6>0,解得x>2或x<-3,综上得2<x<![]() ,即A={x|2<x<
,即A={x|2<x<![]() },
},
∴B=A∪{x|1≤x≤![]() }={x|1≤x<
}={x|1≤x<![]() },又g(x)=-3x2+3x-4=-3(x-
},又g(x)=-3x2+3x-4=-3(x-![]() )2-
)2-![]() 知:g(x)在B上为减函数,∴g(x)max=g(1)=-4.
知:g(x)在B上为减函数,∴g(x)max=g(1)=-4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 <m<
<m<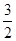 B、
B、 <m<
<m< C、
C、 D、
D、