题目内容
圆x2+y2=8内有一点P(-1,2),AB为过点P且倾斜角为α的弦;(1)当
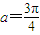 时,求AB的长;
时,求AB的长;(2)当弦AB被点P平分时,求直线AB的方程.
【答案】分析:(1)根据直线的倾斜角求出斜率.因为直线AB过P(-1,2),可表示出直线AB的解析式,利用点到直线的距离公式求出圆心到弦的距离,根据勾股定理求出弦的一半,乘以2得到弦AB的长;
(2)因为弦AB被点P平分,先求出OP的斜率,然后根据垂径定理得到OP⊥AB,由垂直得到两条直线斜率乘积为-1,求出直线AB的斜率,然后写出直线的方程.
解答:解:(1)直线AB的斜率k=tan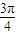 =-1,
=-1,
∴直线AB的方程为y-2=-(x+1),即x+y-1=0
∵圆心O(0,0)到直线AB的距离d=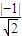 =
=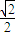
∴弦长|AB|=2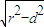 =2
=2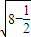 =
=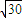 .
.
(2)∵P为AB的中点,OA=OB=r,
∴OP⊥AB
又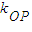 =
=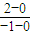 =-2,∴kAB=
=-2,∴kAB=
∴直线AB的方程为y-2= (x+1),即x-2y+5=0
(x+1),即x-2y+5=0
点评:考查学生会根据倾斜角求出直线的斜率,综合运用直线与圆方程的能力,会根据一个点和斜率写出直线的方程.
(2)因为弦AB被点P平分,先求出OP的斜率,然后根据垂径定理得到OP⊥AB,由垂直得到两条直线斜率乘积为-1,求出直线AB的斜率,然后写出直线的方程.
解答:解:(1)直线AB的斜率k=tan
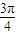 =-1,
=-1,∴直线AB的方程为y-2=-(x+1),即x+y-1=0
∵圆心O(0,0)到直线AB的距离d=
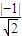 =
=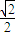
∴弦长|AB|=2
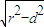 =2
=2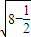 =
=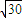 .
.(2)∵P为AB的中点,OA=OB=r,
∴OP⊥AB
又
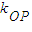 =
=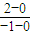 =-2,∴kAB=
=-2,∴kAB=
∴直线AB的方程为y-2=
 (x+1),即x-2y+5=0
(x+1),即x-2y+5=0点评:考查学生会根据倾斜角求出直线的斜率,综合运用直线与圆方程的能力,会根据一个点和斜率写出直线的方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目