题目内容
若f(x)函数为奇函数,且在(0,+∞)内是增函数,又f(2)=0,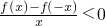 的解集为________.
的解集为________.
解: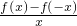 =
=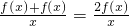 <0,从而
<0,从而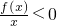
又由已知f(x)函数为奇函数,且在(0,+∞)内是增函数,又f(2)=0,
所以f(x)在(-∞,0)内也是增函数,且f(-2)=0,
因此当0<x<2时,f(x)<0;x>2时,f(x)>0.
当-2<x<0时,f(x)>0;x<-2时,f(x)<0.
若是上述不等式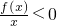 成立,
成立,
必有0<x<2或-2<x<0.
故答案为:(-2,0)∪(0,2)
分析:本题可由奇偶性与单调性得出函数f(x)在另一个单调区间上的性质,然后分别在两个区间上求适合不等式的自变量x的取值范围即可.
点评:本题考查了函数的奇偶性和单调性,奇偶性的应用,函数的定义域与值域的内容,考查了数形结合的思想.
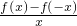 =
=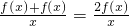 <0,从而
<0,从而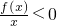
又由已知f(x)函数为奇函数,且在(0,+∞)内是增函数,又f(2)=0,
所以f(x)在(-∞,0)内也是增函数,且f(-2)=0,
因此当0<x<2时,f(x)<0;x>2时,f(x)>0.
当-2<x<0时,f(x)>0;x<-2时,f(x)<0.
若是上述不等式
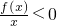 成立,
成立,必有0<x<2或-2<x<0.
故答案为:(-2,0)∪(0,2)
分析:本题可由奇偶性与单调性得出函数f(x)在另一个单调区间上的性质,然后分别在两个区间上求适合不等式的自变量x的取值范围即可.
点评:本题考查了函数的奇偶性和单调性,奇偶性的应用,函数的定义域与值域的内容,考查了数形结合的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目