题目内容
已知点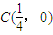 ,椭圆
,椭圆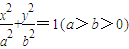 的右准线l1+x=2与x轴相交于点D,右焦点F到上顶点的距离为
的右准线l1+x=2与x轴相交于点D,右焦点F到上顶点的距离为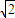 .
.(1)求椭圆的方程;
(2)是否存在过点F且与x轴不垂直的直线l与椭圆交于A、B两点,使得
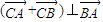 ?若存在,求出直线l;若不存在,说明理由.
?若存在,求出直线l;若不存在,说明理由.
【答案】分析:(1)由题意可得
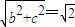 ,a2=b2+c2,从而可求
,a2=b2+c2,从而可求
(2)由(1)得F(1,0),0≤m≤1,假设存在满足条件的直线l:y=k(x-1),代入椭圆方程整理可得(2k2+1)x2-4k2x+2k2-2=0设A(x1,y1),B(x2,y2)设A(x1,y1),B(x2,y2)则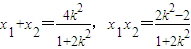 ,
,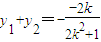 ,由
,由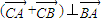 可求k的值
可求k的值
解答:解(1):由题意可得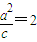
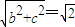 ,a2=b2+c2
,a2=b2+c2
解可得,a2=2,b2=1
所以椭圆方程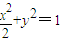
(2)由(1)得F(1,0),0≤m≤1,
假设存在满足条件的直线l:y=k(x-1),代入椭圆方程整理可得(2k2+1)x2-4k2x+2k2-2=0
设A(x1,y1),B(x2,y2)则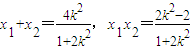
∴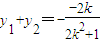
∴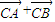 =
=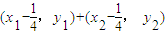 =
=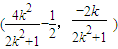 ,
,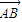 的方向向量(1,k)
的方向向量(1,k)
∴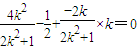
∴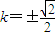 ,
,
所以存在直线l,且直线的方程为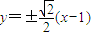
点评:本题主要考查了由椭圆的性质求解椭圆的方程,直线与椭圆相交的位置关系的应用,这是直线与圆锥曲线中的常考的试题类型.

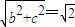 ,a2=b2+c2,从而可求
,a2=b2+c2,从而可求(2)由(1)得F(1,0),0≤m≤1,假设存在满足条件的直线l:y=k(x-1),代入椭圆方程整理可得(2k2+1)x2-4k2x+2k2-2=0设A(x1,y1),B(x2,y2)设A(x1,y1),B(x2,y2)则
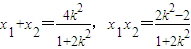 ,
,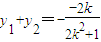 ,由
,由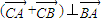 可求k的值
可求k的值解答:解(1):由题意可得
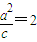
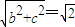 ,a2=b2+c2
,a2=b2+c2解可得,a2=2,b2=1
所以椭圆方程
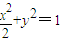
(2)由(1)得F(1,0),0≤m≤1,
假设存在满足条件的直线l:y=k(x-1),代入椭圆方程整理可得(2k2+1)x2-4k2x+2k2-2=0
设A(x1,y1),B(x2,y2)则
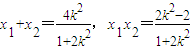
∴
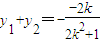
∴
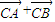 =
=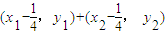 =
=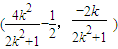 ,
, 的方向向量(1,k)
的方向向量(1,k)∴
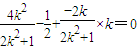
∴
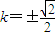 ,
,所以存在直线l,且直线的方程为
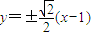
点评:本题主要考查了由椭圆的性质求解椭圆的方程,直线与椭圆相交的位置关系的应用,这是直线与圆锥曲线中的常考的试题类型.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
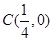 ,椭圆
,椭圆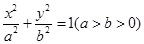 的右准线
的右准线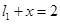 与x轴相交于点D,右焦点F到上顶点的距离为
与x轴相交于点D,右焦点F到上顶点的距离为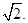
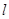 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得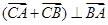 ?若存在,求出直线
?若存在,求出直线 ,椭圆
,椭圆 的右准线l1+x=2与x轴相交于点D,右焦点F到上顶点的距离为
的右准线l1+x=2与x轴相交于点D,右焦点F到上顶点的距离为 .
. ?若存在,求出直线l;若不存在,说明理由.
?若存在,求出直线l;若不存在,说明理由.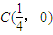 ,椭圆
,椭圆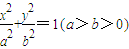 的右准线l1+x=2与x轴相交于点D,右焦点F到上顶点的距离为
的右准线l1+x=2与x轴相交于点D,右焦点F到上顶点的距离为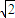 .
.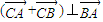 ?若存在,求出直线l;若不存在,说明理由.
?若存在,求出直线l;若不存在,说明理由.