题目内容
用模型f(x)=ax+b来描述某企业每季度的利润f(x)(亿元)和生产成本投入x(亿元)的关系.统计表明,当每季度投入1(亿元)时利润y1=1(亿元),当每季度投入2(亿元)时利润y2=2(亿元),当每季度投入3(亿元)时利润y3=2(亿元).又定义:当f(x)使[f(1)-y1]2+[f(2)-y2]2+[f(3)-y3]2的数值最小时为最佳模型.(1)若b=
| 2 | 3 |
(2)根据题(1)得到的最佳模型,请预测每季度投入4(亿元)时利润y4(亿元)的值.
分析:(1)当f(x)使[f(1)-y1]2+[f(2)-y2]2+[f(3)-y3]2的数值最小时为最佳模型,把条件中所给的数值代入,整理出关于a的二次函数,得到结果.
(2)根据上一问做出的a的值,和所给的b的值,写出关于利润f(x)(亿元)和生产成本投入x(亿元)的关系式,把所给的x=4代入,得到y的值.
(2)根据上一问做出的a的值,和所给的b的值,写出关于利润f(x)(亿元)和生产成本投入x(亿元)的关系式,把所给的x=4代入,得到y的值.
解答:解:(1)∵当f(x)使[f(1)-y1]2+[f(2)-y2]2+[f(3)-y3]2的数值最小时为最佳模型
b=
时[f(1)-y1]2+[f(2)-y2]2+[f(3)-y3]2=14(a-
)2+
∴a=
时,函数为最佳模型
(2)∵a=
,
∴f(x)=
x+b,
∵b=
∴f(x)=
x+
,
∴当x=4时有y4=f(4)=
b=
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
∴a=
| 1 |
| 2 |
(2)∵a=
| 1 |
| 2 |
∴f(x)=
| 1 |
| 2 |
∵b=
| 2 |
| 3 |
∴f(x)=
| 1 |
| 2 |
| 2 |
| 3 |
∴当x=4时有y4=f(4)=
| 8 |
| 3 |
点评:本题考查函数模型的选择和应用,本题解题的关键是读懂题意,看清楚本题所定义的最简模型的运算,本题是一个比较新颖的题目.

练习册系列答案
相关题目
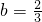 ,求相应的a使f(x)=ax+b成为最佳模型;
,求相应的a使f(x)=ax+b成为最佳模型;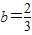 ,求相应的a使f(x)=ax+b成为最佳模型;
,求相应的a使f(x)=ax+b成为最佳模型;