Question

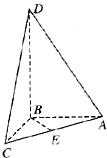（2000•上海）如图所示四面体ABCD中，AB、BC、BD两两互相垂直，且AB=BC=2，E是AC中点，异面直线AD与BE所成的角的大小为arccos

10

10

，求四面体ABCD的体积．

Answer 1

分析：建立如图所示坐标系，得A、B、C、D各点的坐标，利用向量数量积的公式结合AD、BE所成角为arccos

10

10

，解出BD的长度是4，最后运用锥体的体积公式即可算出四面体ABCD的体积．

解答：解：以BC、BA、BD为x轴、y轴、z轴，建立如图所示空间直角坐标系，…（2分）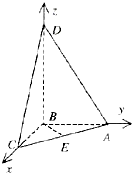
由题意得A（0，2，0），C（2，0，0），E（1，1，0）
设D点的坐标为（0，0，z）（z＞0），
则

BE

=(1，1，0)，

AD

=(0，-2，z)…（6分）
∴

AD

•

BE

=

2

•

4+z2

cosθ=-2，
∵AD与BE所成的角的大小为arccos

10

10

，可得cos2θ=

2

4+z2

=

1

10

，
∴代入上式，解之得z=4，即BD的长度是4，…（10分）
因此，三棱锥D-ABC的体积
VD-ABC=

1

3

S△ABC•BD=

1

6

AB•BC•BD=

1

6

×2×2×4=

8

3

，
即四面体ABCD的体积是

8

3

，…（12分）

点评：本题给出特殊三棱锥，在已知异面直线所成角的基础之上求锥体的体积．着重考查了利用空间坐标系的方法研究异面直线所成角和锥体的体积公式等知识，属于中档题．