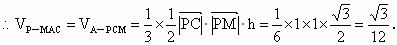题目内容
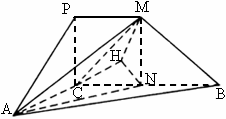
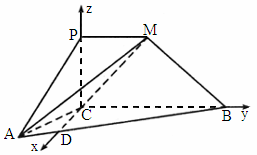
(2007四川,19)如下图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1.∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
(1)求证:平面PAC⊥平面ABC;
(2)求二面角M-AC-B的大小;
(3)求三棱锥P-MAC的体积.
答案:略
解析:
解析:
|
解析:解法一:(1)∵PC⊥AB,PC⊥BC,
∴PC⊥平面ABC.又∵PC ∴平面PAC⊥平面ABC. (2)取BC的中点N,则CN=1. 连结AN、MN,∵ ∴ 作NH⊥AC,交AC的延长线于H,连结MH,则由三垂线定理知,AC⊥MH,从而∠MHN为二面角M-AC-B的平面角. ∵直线AM与直线PC所成的角为60°, ∴∠AMN=60°. 在△ACN中,由余弦定理得
在Rt△AMN中,
在Rt△MNH, 故二面角M-AC-B的大小为 (3)由(2)知,PCNM为正方形,
解法二:(1)同解法一. (2)在平面ABC内,过C作CD⊥CB.建立空间直角坐标系C-xyz(如图),
由题意有 设
由直线AM与直线PC所成的角为60°, 得 即
平面MAC的一个法向量为
则 得 平面ABC的法向量取为m=(0,0,1). 设m与n所成角为θ, 则 (3)取平面PCM的法向量为 则点A到平面PCM的距离 因
|

练习册系列答案
相关题目
 ,
,
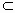 平面PAC,
平面PAC,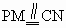 .
.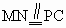 ,从而MN⊥平面ABC.
,从而MN⊥平面ABC.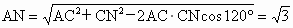 .
. .在Rt△CNH中,
.在Rt△CNH中,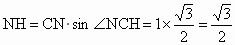 .
.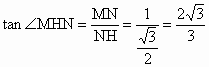 .
. .
.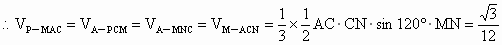 .
.
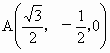 .
.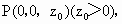 则
则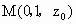 ,
,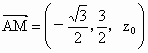 ,
,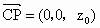 .
.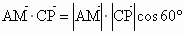 ,
, ,解得
,解得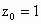 .
.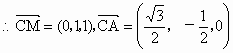 ,设
,设 .
. 取
取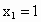 ,
,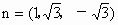 .
.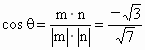 ,显然,二面角M-AC-B的平面角为锐角,故二面角M-AC-B的大小为
,显然,二面角M-AC-B的平面角为锐角,故二面角M-AC-B的大小为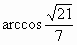 .
.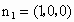 ,
, .
.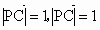 ,
,